
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
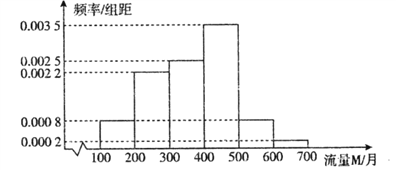
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
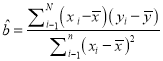 ,
, ![]()
【答案】(Ⅰ)0.75;(Ⅱ)369M;(Ⅲ) ![]() .
.
【解析】试题分析:(I)直接根据二项分布的期望公式求解即可;(II)根据频率分布直方图中数据,每组数据中间值与纵坐标的乘积之和即是被抽查的居民使用流量的平均值;(Ⅲ)先根据平均值公式求出样本中心点的坐标,利用公式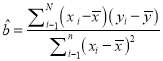 求出
求出![]() ,样本中心点坐标代入回归方程可得
,样本中心点坐标代入回归方程可得![]() ,从而可得结果.
,从而可得结果.
试题解析:(Ⅰ)依题意, ![]() ∽
∽![]() ,故
,故![]() ;
;
(Ⅱ)依题意,所求平均数为![]() 故所用流量的平均值为
故所用流量的平均值为![]() ;
;
(Ⅲ)由题意可知![]() ,
,
![]() ,
,
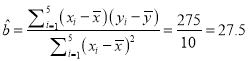 ,
,
![]() 所以,
所以, ![]() 关于
关于![]() 的回归方程为:
的回归方程为: ![]() .
.
【方法点晴】本题主要考查二项分布的期望公式、直方图的应用和线性回归方程的求法,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ; 回归直线过样本点中心
; 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


科目:高中数学 来源: 题型:
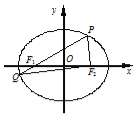
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设
(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设![]() =λ
=λ![]() .
.
(1)若点P的坐标为(1,![]() ),且△PQF2的周长为8,求椭圆C的方程;
),且△PQF2的周长为8,求椭圆C的方程;
(2)若PF2垂直于x轴,且椭圆C的离心率e∈[![]() ,
,![]() ],求实数λ的取值范围.
],求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 是曲线
是曲线![]() 与直线
与直线![]() :
: ![]() (
(![]() )的交点(异于原点
)的交点(异于原点![]() ).
).
(1)写出![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)求过点![]() 和直线
和直线![]() 垂直的直线
垂直的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,
为常数, ![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,判断方程
时,判断方程![]() 是否有实根?若无实根请说明理由,若有实根请给出根的个数.
是否有实根?若无实根请说明理由,若有实根请给出根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-f′(0)ex+2x,点P为曲线y=f(x)在点(0,f(0))处的切线l上的一点,点Q在曲线y=ex上,则|PQ|的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com