
【题目】设函数f(x)=![]() ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).
(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y=![]() 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;
(3)设h(x)=|af2(x)﹣![]() |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党的群众教育路线总结阶段,一督导组从某单位随机抽调25名员工,让他们对单位的各项开展工作进行打分评价,现获得如下数据:70,82,81,76,84,80,77,77,65,85,69,83,71,76,89,74,73,83,78,82,72,74,86,79,76.
(1)根据上述数据完成样本的频率分布表;
(2)根据(1)的频率分布表,完成样本分布直方图;
(3)从区间![]() 和
和![]() 中任意抽取两个评分,求两个评分来自不同区间的概率.
中任意抽取两个评分,求两个评分来自不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数
求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数
(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
(I)每组两本
(II)一组一本,一组二本,一组三本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题。”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论。现从该班随机抽取5位学生在一次考试中的数学和物理成绩,如下表:

(1)求数学成绩y对物理成绩x的线性回归方程![]() 。若某位学生的物理成绩为80分,预测他的数学成绩;
。若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这5位学生中随机抽取2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率。(参考公式:  参考数据:
参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取![]() 名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于
名学生的成绩进行统计,作出的茎叶图如下图,记成绩不低于![]() 分者为“成绩优良”.
分者为“成绩优良”.

(1)分别计算甲、乙两班![]() 个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
个样本中,化学分数前十的平均分,并据此判断哪种教学方式的教学效果更
佳;
(2)甲、乙两班![]() 个样本中,成绩在
个样本中,成绩在![]() 分以下(不含
分以下(不含![]() 分)的学生中任意选取
分)的学生中任意选取![]() 人,求这
人,求这![]() 人来自不同班级的概率;
人来自不同班级的概率;
(3)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: 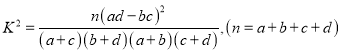
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com