
分析 (1)根据题意得出,b2=ac,利用余弦定理,基本不等式求解cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}}{2ac}$-$\frac{1}{2}$≥$\frac{1}{2}$,根据余弦函数的单调性得出答案.
(2)利用三角函数恒等变换的应用化简可得y=$\frac{\sqrt{2}}{2}$sin(B+$\frac{π}{4}$)-$\frac{1}{2}$,由B∈(0,$\frac{π}{3}$],可得B+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{7π}{12}$],利用正弦函数的图象和性质可求sin(B+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,1],即可得解y的范围.
解答 解:(1)∵△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,已知a,b,c成等比数列,
∴cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,b2=ac,
∵a2+c2≥2ac(a=c等号成立),
∴$\frac{{a}^{2}+{c}^{2}}{2ac}$≥1,
∴cos∠B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}}{2ac}$-$\frac{1}{2}$≥$\frac{1}{2}$,
∵0<B<π,y=cosB单调递减,
∴B∈(0,$\frac{π}{3}$].
(2)y=$\frac{sinB•cosB}{1+sinB+cosB}$=$\frac{2sin\frac{B}{2}cos\frac{B}{2}cosB}{2cos\frac{B}{2}(sin\frac{B}{2}+cos\frac{B}{2})}$=$\frac{sin\frac{B}{2}cosB}{sin\frac{B}{2}+cos\frac{B}{2}}$=$\frac{sin\frac{B}{2}cosB(cos\frac{B}{2}-sin\frac{B}{2})}{cosB}$=$\frac{1}{2}$(sinB+cosB)-$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$sin(B+$\frac{π}{4}$)-$\frac{1}{2}$.
∵B∈(0,$\frac{π}{3}$].B+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{7π}{12}$],sin(B+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,1],
∴y=$\frac{sinB•cosB}{1+sinB+cosB}$=$\frac{\sqrt{2}}{2}$sin(B+$\frac{π}{4}$)-$\frac{1}{2}$∈(0,$\frac{\sqrt{2}-1}{2}$].
点评 本题考查等比数列的性质,正弦函数的图象和性质,考查了三角函数恒等变换的应用,考查了运用余弦定理,基本不等式求解,属于中档题.


科目:高中数学 来源: 题型:解答题
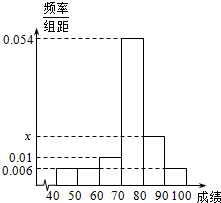 某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,1) | C. | (-∞,4] | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com