
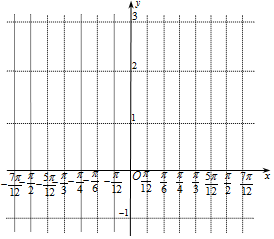
 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4}{3}$π | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2}{3}$π |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
分析 (1)先把数据补全,利用描点法能在给出的直角坐标系中,画出f(x)在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
(2)利用正弦函数的图象及性质能求出函数$f(x)=2sin(2x-\frac{π}{3})+1$的最小值及取最小值时x的集合.
(3)当$x∈[0,\frac{π}{2}]$时,$2x-\frac{π}{3}∈[-\frac{π}{3},\frac{2π}{3}]$,从而$sin(2x-\frac{π}{3})∈[{-\frac{{\sqrt{3}}}{2},1}]$,由此能求出f(x)在$x∈[0,\frac{π}{2}]$时的值域.
解答 解:(1)数据补全如下表:
| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) | $\sqrt{3}+1$ | 1 | -1 | 1 | 3 | $\sqrt{3}+1$ |
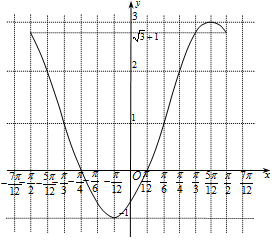
点评 本题考查三角函数的图象的画法,考查三角函数的最小值及取最小值时x的集合的求法,考查三角函数的值域的求法,涉及到三角函数的图象及性质等知识点,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
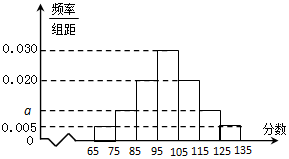 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a>b>c | C. | c>a>b | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15,20,25 | B. | 5,12,31,39,57 | C. | 6,16,26,36,46 | D. | 6,18,30,42,54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=33y | B. | x2=33y | C. | x2=8y | D. | x2=16y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com