
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分,众数,中位数;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在[50,90)之外的人数.
)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| 1:1 | 2:1 | 3:4 | 4:5 |

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若![]() q是
q是![]() p的必要不充分条件,求实数a的取值范围.
p的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a,b,c.角A,B,C成等差数列.
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 参数方程为
参数方程为 (
(![]() 为参数,
为参数,![]() ),以坐标原点为极点,以
),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,曲线
,曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,已知AB=AC=AA1= ![]() ,BC=4,点A1在底面ABC的投影是线段BC的中点O.
,BC=4,点A1在底面ABC的投影是线段BC的中点O. 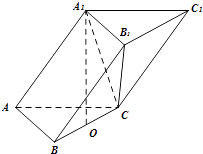
(1)证明在侧棱AA1上存在一点E,使得OE⊥平面BB1C1C,并求出AE的长;
(2)求平面A1B1C与平面BB1C1C夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数h(x)满足
①h(0)=1,h(1)=0;
②对任意a∈[0,1],有h(h(a))=a;
③在(0,1)上单调递减.则称h(x)为补函数.已知函数h(x)= ![]() (λ>﹣1,p>0)
(λ>﹣1,p>0)
(1)判函数h(x)是否为补函数,并证明你的结论;
(2)若存在m∈[0,1],使得h(m)=m,若m是函数h(x)的中介元,记p= ![]() (n∈N+)时h(x)的中介元为xn , 且Sn=
(n∈N+)时h(x)的中介元为xn , 且Sn= ![]() ,若对任意的n∈N+ , 都有Sn<
,若对任意的n∈N+ , 都有Sn< ![]() ,求λ的取值范围;
,求λ的取值范围;
(3)当λ=0,x∈(0,1)时,函数y=h(x)的图象总在直线y=1﹣x的上方,求P的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx﹣ ![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标. 
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某共享单车企业在![]() 城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:
城市就“一天中一辆单车的平均成本与租用单车数量之间的关系”进行了调查,并将相关数据统计如下表:

根据以上数据,研究人员设计了两种不同的回归分析模型,得到两个拟合函数:
模型甲:![]() ,模型乙:
,模型乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1元)(备注:![]() ,
,![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);

②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这家企业在4城市投放共享单车后,受到广大市民的热烈欢迎并供不应求,于是该企业决定增加单车投放量.根据市场调查,市场投放量达到1万辆时,平均每辆单车一天能收入7.2元;市场投放量达到1.2万辆时,平均每辆单车一天能收入6.8元.若按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,问该企业投放量选择1万辆还是1.2万辆能获得更多利润?请说明理由.(利润![]() 收入
收入![]() 成本)
成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com