
分析 (1)依题意知an>0,故an+1>an+$\frac{a_n^2}{n^2}$>an,ak+1=ak+$\frac{a_k^2}{k^2}$<ak+$\frac{{{a_k}{a_{k+1}}}}{k^2}$,从而可得$\frac{1}{a_k}-\frac{1}{{{a_{k+1}}}}<\frac{1}{k^2}$,累加可证结论成立;
(2)分n=1与n≥2两类讨论,对于后者,利用放缩法即可证得${a_n}≥\frac{n}{2n+1}$(n∈N*).
解答 (本题满分15分)
证明:(I)易知an>0,所以an+1>an+$\frac{a_n^2}{n^2}$>an,
所以 ak+1=ak+$\frac{a_k^2}{k^2}$<ak+$\frac{{{a_k}{a_{k+1}}}}{k^2}$,
所以$\frac{1}{a_k}-\frac{1}{{{a_{k+1}}}}<\frac{1}{k^2}$.
所以,当n≥2时,$\frac{1}{a_n}=\frac{1}{a_1}-\sum_{k=1}^{n-1}{(\frac{1}{a_k}-\frac{1}{{{a_{k+1}}}})}>\frac{1}{a_1}-\sum_{k=1}^{n-1}{\frac{1}{k^2}}>3-[1+\sum_{k=2}^{n-1}{\frac{1}{k(k-1)}}]=3-[1+\sum_{k=2}^{n-1}{(\frac{1}{k-1}-\frac{1}{k})}]$=$3-[1+1-\frac{1}{n-1}]=\frac{n}{n-1}>1$,
所以an<1.
又${a_1}=\frac{1}{3}<1$,所以an<1(n∈N*),
所以 an<an+1<1(n∈N*).…(8分)
(II)当n=1时,显然成立.
由an<1,知${a_{k+1}}={a_k}+\frac{a_k^2}{k^2}<{a_k}+\frac{a_k}{k^2}$,所以${a_k}>\frac{k^2}{{{k^2}+1}}{a_{k+1}}$,
所以${a_{k+1}}={a_k}+\frac{a_k^2}{k^2}>{a_k}+\frac{1}{k^2}{a_k}•\frac{k^2}{{{k^2}+1}}{a_{k+1}}={a_k}+\frac{1}{{{k^2}+1}}{a_k}{a_{k+1}}$,
所以$\frac{1}{a_k}-\frac{1}{{{a_{k+1}}}}>\frac{1}{{{k^2}+1}}$,
所以,当n≥2时,$\frac{1}{a_n}=\frac{1}{a_1}-\sum_{k=1}^{n-1}{(\frac{1}{a_k}-\frac{1}{{{a_{k+1}}}})}<\frac{1}{a_1}-\sum_{k=1}^{n-1}{\frac{1}{{{k^2}+1}}}<3-\sum_{k=1}^{n-1}{\frac{1}{k(k+1)}}=3-\sum_{k=1}^{n-1}{(\frac{1}{k}-\frac{1}{k+1})}$
=$3-(1-\frac{1}{n})=\frac{2n+1}{n}$,即${a_n}>\frac{n}{2n+1}$.
所以${a_n}≥\frac{n}{2n+1}$(n∈N*). …(7分)
点评 本题考查数列递推式,突出考查等放缩法证明不等式的应用,考查转化思想与推理运算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -π | B. | -$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| B. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| C. | 命题“若a=-b,则|a|=|b|”的否命题是真命题 | |
| D. | 命题“若$\left\{{\overrightarrow a,\overrightarrow b,\overrightarrow c}\right\}$为空间的一个基底,则$\left\{{\overrightarrow a+\overrightarrow b,\overrightarrow b+\overrightarrow c,\overrightarrow c+\overrightarrow a}\right\}$构成空间的另一个基底”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
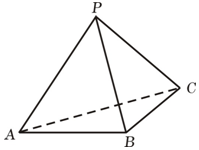 如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.
如图,三棱锥P-ABC中,△ABC为等腰直角三角形,AB=BC=2,PA=PB=PC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com