
ĄūĖâÄŋĄŋąĢŧĪŧ·ūģĢŽ·ĀÖÎŧ·ūģÎÛČūÔ―ĀīÔ―ĩÃĩ―ČËÃĮĩÄÖØĘÓĢŽÄģÆóŌĩÔÚÏÖÓÐÉčąļÏÂÃŋČÕÉúēúŨÜģÉąū![]() ĢĻĩĨÎŧĢšÍōÔŠĢĐÓëČÕēúÁŋ
ĢĻĩĨÎŧĢšÍōÔŠĢĐÓëČÕēúÁŋ![]() ĢĻĩĨÎŧĢšķÖĢĐÖŪžäĩÄšŊĘýđØÏĩĘ―ÎŠ
ĢĻĩĨÎŧĢšķÖĢĐÖŪžäĩÄšŊĘýđØÏĩĘ―ÎŠ![]() ĢŪÏÖΊÁËžõÉŲīóÆøÎÛČūĢŽļÃÆóŌĩŌý―øÁËģýģūÉčąļĢŽÃŋķÖēúÆ·ģýģū·ŅÓÃΊ
ĢŪÏÖΊÁËžõÉŲīóÆøÎÛČūĢŽļÃÆóŌĩŌý―øÁËģýģūÉčąļĢŽÃŋķÖēúÆ·ģýģū·ŅÓÃΊ![]() ÍōÔŠĢŽģýģūšóĢŽĩąČÕēúÁŋ
ÍōÔŠĢŽģýģūšóĢŽĩąČÕēúÁŋ![]() ĘąĢŽÃŋČÕÉúēúŨÜģÉąū
ĘąĢŽÃŋČÕÉúēúŨÜģÉąū![]() ĢŪ
ĢŪ
ĢĻ1ĢĐĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ2ĢĐČôÃŋķÖēúÆ·ģöģ§žÛΊ48ÍōÔŠĢŽĘÔĮóģýģūšóČÕēúÁŋΊķāÉŲķÖĘąĢŽÃŋķÖēúÆ·ĩÄĀûČóŨîīóĢŽŨîīóĀûČóΊķāÉŲÍōÔŠĢŋ
Ąūīð°ļĄŋĢĻ1ĢĐkĢ―2Ģŧ ĢĻ2ĢĐČÕēúÁŋΊ4ķÖĘąĢŽÃŋķÖēúÆ·ĩÄĀûČóŨîīóĢŽŨîīóĀûČóΊ26ÍōÔŠĢŪ
Ąū―âÎöĄŋ
ĢĻ1ĢĐĮóģöģýģūšóĩÄšŊĘý―âÎöĘ―ĢŽĀûÓÃĩąČÕēúÁŋ![]() ĘąĢŽŨÜģÉąū
ĘąĢŽŨÜģÉąū![]() ĢŽīúČëžÆËãĩÃ
ĢŽīúČëžÆËãĩÃ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐĮóģöÃŋķÖēúÆ·ĩÄĀûČóĢŽĀûÓÃŧųąūēŧĩČĘ―Įó―âžīŋÉĢŪ
―âĢšĢĻ1ĢĐÓÉĖâŌâĢŽģýģūšó![]() ĢŽ
ĢŽ
―Ŧ![]() ĢŽ
ĢŽ![]() īúČëĩÃ
īúČëĩÃ![]() ―âĩÃ
―âĩÃ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐÓÉĢĻ1ĢĐÖĩ![]() ĢŽŨÜĀûČó
ĢŽŨÜĀûČó![]() ĢŽ
ĢŽ
ÔōÃŋķÖēúÆ·ĩÄĀûČó![]() ĢŽ
ĢŽ
ĩąĮŌ―öĩą![]() ĢŽžī
ĢŽžī![]() ʹȥĩČšÅĢŽ
ʹȥĩČšÅĢŽ
ËųŌÔģýģūšóČÕēúÁŋΊ![]() ķÖĘąĢŽÃŋķÖēúÆ·ĩÄĀûČóŨîīóĢŽŨîīóĀûČóΊ
ķÖĘąĢŽÃŋķÖēúÆ·ĩÄĀûČóŨîīóĢŽŨîīóĀûČóΊ![]() ÍōÔŠĢŪ
ÍōÔŠĢŪ


 ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ
ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĘýŅ§žŌÅ·ĀÔÚ1765ÄęĖáģöĢšČý―ĮÐÎĩÄÍâÐÄĄĒÖØÐÄÎŧÓÚÍŽŌŧÖąÏßÉÏĢŽÕâĖõÖąÏßąŧšóČËģÆÖŪΊČý―ĮÐÎĩÄÅ·ĀÏßĢŽČô![]() ĩÄķĨĩã
ĩÄķĨĩã![]() ĢŽ
ĢŽ![]() ĢŽĮŌ
ĢŽĮŌ![]() ĩÄÅ·ĀÏßĩÄ·―ģĖΊ
ĩÄÅ·ĀÏßĩÄ·―ģĖΊ![]() .
.
ĢĻ1ĢĐĮó![]() ÍâÐÄ
ÍâÐÄ![]() ĢĻÍâ―ÓÔēÔēÐÄĢĐĩÄŨøąęĢŧ
ĢĻÍâ―ÓÔēÔēÐÄĢĐĩÄŨøąęĢŧ
ĢĻ2ĢĐĮóķĨĩã![]() ĩÄŨøąę.
ĩÄŨøąę.
ĢĻŨĒĢšČįđû![]() ČýļöķĨĩãŨøąę·ÖąðΊ
ČýļöķĨĩãŨøąę·ÖąðΊ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÔō
ĢŽÔō![]() ÖØÐÄĩÄŨøąęĘĮ
ÖØÐÄĩÄŨøąęĘĮ![]() .ĢĐ
.ĢĐ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() ĢŽ
ĢŽ![]() .
.
ĢĻ1ĢĐČôšŊĘý![]() ÔÚ
ÔÚ![]() īĶĩÄĮÐÏßÓëÖąÏß
īĶĩÄĮÐÏßÓëÖąÏß![]() Æ―ÐÐĢŽĮóĘĩĘý
Æ―ÐÐĢŽĮóĘĩĘý![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ2ĢĐĘÔĖÖÂÛšŊĘý![]() ÔÚĮøžä
ÔÚĮøžä![]() ÉÏŨîīóÖĩĢŧ
ÉÏŨîīóÖĩĢŧ
ĢĻ3ĢĐČô![]() ĘąĢŽšŊĘý
ĘąĢŽšŊĘý![]() ĮĄÓÐÁ―ļöÁãĩã
ĮĄÓÐÁ―ļöÁãĩã![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() .
.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽģĪ·―ĖåABCDĐA1B1C1D1ÖÐĢŽADĢ―AA1Ģ―1ĢŽABĢ―2ĢŽĩãEĘĮÏßķÎABÖÐĩã.

ĢĻ1ĢĐÖĪÃũĢšD1EĄÍCEĢŧ
ĢĻ2ĢĐĮóķþÃæ―ĮD1ĐECĐDĩÄīóÐĄĩÄÓāÏŌÖĩĢŧ
ĢĻ3ĢĐĮóAĩãĩ―Æ―ÃæCD1EĩÄūāĀë.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÏÂąíĖáđĐÁËÄģģ§―ÚÄÜ―ĩšÄžžĘõļÄÔėšóÉúēúžŨēúÆ·đýģĖÖОĮžĩÄēúÁŋ![]() (ķÖ)ÓëÏāÓĶĩÄÉúēúÄÜšÄ
(ķÖ)ÓëÏāÓĶĩÄÉúēúÄÜšÄ![]() (ķÖ)ąęŨžÃšĩÄžļŨéķÔÕÕĘýūÝ
(ķÖ)ąęŨžÃšĩÄžļŨéķÔÕÕĘýūÝ
|
|
|
|
|
|
|
|
|
|
(1)ĮëļųūÝÉÏąíĖáđĐĩÄĘýūÝĢŽÓÃŨîÐĄķþģË·ĻĮóģö![]() đØÓÚ
đØÓÚ![]() ĩÄÏßÐÔŧØđé·―ģĖ
ĩÄÏßÐÔŧØđé·―ģĖ![]() Ģŧ
Ģŧ
(2)ŌŅÖŠļÃģ§žžļÄĮ°100ķÖžŨēúÆ·ĩÄÉúēúÄÜšÄΊ90ķÖąęŨžÃšĢŪĘÔļųūÝ(1)ĮóģöĩÄÏßÐÔŧØđé·―ģĖĢŽÔĪēâÉúēú100ķÖžŨēúÆ·ĩÄÉúēúÄܚĹȞžļÄĮ°―ĩĩÍķāÉŲķÖąęŨžÃš?
ēÎŋžđŦĘ―Ģš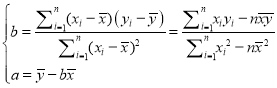
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚËÄĀâŨķ![]() ÖÐĢŽ
ÖÐĢŽ![]() Æ―Ãæ
Æ―Ãæ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() .
.![]() ΊÏßķÎ
ΊÏßķÎ![]() ÉÏĩÄĩã.
ÉÏĩÄĩã.

ĢĻIĢĐÖĪÃũĢš![]() Ãæ
Ãæ![]()
ĢĻĒōĢĐČô![]() ĘĮ
ĘĮ![]() ĩÄÖÐĩãĢŽĮó
ĩÄÖÐĩãĢŽĮó![]() ÓëÆ―Ãæ
ÓëÆ―Ãæ![]() ËųģÉĩÄ―ĮĩÄÕýÏŌÖĩ;
ËųģÉĩÄ―ĮĩÄÕýÏŌÖĩ;
ĢĻĒóĢĐČô![]() ÂúŨã
ÂúŨã![]() Ãæ
Ãæ![]() ĢŽĮóķþÃæ―Į
ĢŽĮóķþÃæ―Į![]() ÕýÏŌÖĩ.
ÕýÏŌÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÉčšŊĘý![]() ĢŽ
ĢŽ![]() ĢŪ
ĢŪ
ĢĻ1ĢĐČôšŊĘýfĢĻxĢĐÔÚ![]() īĶÓОŦÖĩĢŽĮóšŊĘýfĢĻxĢĐĩÄŨîīóÖĩĢŧ
īĶÓОŦÖĩĢŽĮóšŊĘýfĢĻxĢĐĩÄŨîīóÖĩĢŧ
ĢĻ2ĢĐĘĮ·ņīæÔÚĘĩĘýbĢŽĘđĩÃđØÓÚxĩÄēŧĩČĘ―![]() ÔÚ
ÔÚ![]() ÉÏšãģÉÁĒĢŋČôīæÔÚĢŽĮóģöbĩÄČĄÖĩ·ķΧĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŧ
ÉÏšãģÉÁĒĢŋČôīæÔÚĢŽĮóģöbĩÄČĄÖĩ·ķΧĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŧ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģÐĢŅ§ÉúÉįÍÅŨéÖŊŧîķŊ·áļŧĢŽŅ§ÉúŧáΊÁË―âÍŽŅ§ķÔÉįÍÅŧîķŊĩÄÂúŌâģĖķČĢŽËæŧúŅĄČĄÁË100ÎŧÍŽŅ§―øÐÐÎĘūíĩũēéĢŽēĒ―ŦÎĘūíÖÐĩÄÕâ100ČËļųūÝÆäÂúŌâķČÆĀ·ÖÖĩĢĻ°Ų·ÖÖÆĢĐ°īÕÕ[40ĢŽ50ĢĐĢŽ[50ĢŽ60ĢĐĢŽ[60ĢŽ70ĢĐĢŽĄĢŽ[90ĢŽ100]·ÖģÉ6ŨéĢŽÖÆģÉČįÍžËųĘūÆĩÂĘ·ÖēžÖą·―ÍžĢŪ
ĢĻ1ĢĐĮóÍžÖÐxĩÄÖĩĢŧ
ĢĻ2ĢĐĮóÕâŨéĘýūÝĩÄÖÐÎŧĘýĢŧ
ĢĻ3ĢĐÏÖīÓąŧĩũēéĩÄÎĘūíÂúŌâķČÆĀ·ÖÖĩÔÚ[60ĢŽ80ĢĐĩÄŅ§ÉúÖаī·ÖēãģéŅųĩÄ·―·ĻģéČĄ5ČË―øÐÐŨųĖļÁË―âĢŽÔŲīÓÕâ5ČËÖÐËæŧúģéČĄ2ČËŨũÖũĖâ·ĒŅÔĢŽĮóģéČĄĩÄ2ČËĮĄÔÚÍŽŌŧŨéĩÄļÅÂĘĢŪ

ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com