
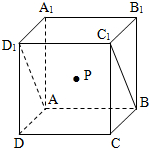
 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在正方体ABCD-A1B1C1D1中,点P是对角面ABC1D1内一动点,若点P到直线AD1距离与点P到平面ABCD的距离相等,则动点P的轨迹所在的曲线类型是( )
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在正方体ABCD-A1B1C1D1中,点P是对角面ABC1D1内一动点,若点P到直线AD1距离与点P到平面ABCD的距离相等,则动点P的轨迹所在的曲线类型是( )| A、直线 | B、椭圆 | C、双曲线 | D、抛物线 |
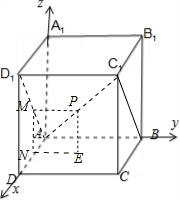 建立空间直角坐标系.
建立空间直角坐标系.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的 倍,则动点P的轨迹所在的曲线类型是
倍,则动点P的轨迹所在的曲线类型是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com