

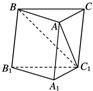
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C.
(3)AM=MA1是截面MBC1⊥侧面BB1C1C的充要条件吗?请你叙述判断理由.
解析:(1)证明:∵AB=AC,D是BC中点,∴AD⊥BC.?
∵底面ABC⊥侧面BB1C1C,交线为BC,?
∴由面面垂直的性质定理可知AD⊥侧面BB1C1C.?
又∵CC1![]() 侧面BB1C1C,∴AD⊥CC1.?
侧面BB1C1C,∴AD⊥CC1.?
(2)证法一:延长B1A1与BM交于N(在侧面AA1B1B中),连结C1N.?
∵AM=MA1,∴NA1=A1B1.?
又∵A1B1=A1C1,由棱柱定义知△ABC≌△A1B1C1,?
∴AB=A1B1,AC=A1C1.?
∴A1C1=A1N=A1B1.?
∴在△B1C1N中,由平面几何定理知∠NC1B1=90°,?
即C1N⊥B1C1.?
又∵侧面BB1C1C⊥底面A1B1C1,交线为B1C1,?
∴NC1⊥侧面BB1C1C.?
又∵NC1![]() 面BNC1,∴截面C1NB⊥侧面BB1C1C.?
面BNC1,∴截面C1NB⊥侧面BB1C1C.?
?∴截面MBC1⊥侧面BB1C1C.?
证法二:取BC1中点E,连结DE、ME.在△BCC1中,D、E分别是BC、BC1中点,∴DE ![]()
![]() CC1.?
CC1.?
又AA1![]() CC1,∴DE
CC1,∴DE![]()
![]() AA1.?
AA1.?
∵M是AA1的中点(由AM=MA1知),∴DE ![]() AM.?
AM.?
∴AMED是平行四边形.?
∴AD![]() ME.?
ME.?
由(1)知AD⊥面BB1C1C,∴ME⊥侧面BB1C1C.?
又∵ME![]() 面BMC1,
面BMC1,
∴面BMC1⊥侧面BB1C1C.?
(3)结论是肯定的,充分性已由(2)证明.下面仅证明必要性(即由截面BMC1⊥侧面BB1C1C,推出AM=MA1,实质证明M是AA1中点).?
过M作ME1⊥BC1于E1.?
∵截面MBC1⊥侧面BB1C1C,交线为BC1,?
∴ME1⊥面BB1C1C.?
又由(1)知AD⊥侧面BB1C1C.?
∵同垂直于一个平面的两条直线平行,
∴AD∥MB1.?
∴M、E1、D、A四点共面.?
又∵AM∥侧面BB1C1C,面AME1D∩面BB1C1C=DE1,∴由线面平行的性质定理可知AM∥DE1.
又AD∥ME1,∴四边形AME1D是平行四边形.?
∴AD=ME1,DE1 ![]() AM.?
AM.?
又∵AM∥CC1,∴DE1∥CC1.?
又∵D是BC中点,∴E1是BC1中点.?
∴DE1=12CC1=12AA1.?
∴AM=12AA1.?
∴MA=MA1.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
| A、直线AB上 | B、直线BC上 | C、直线CA上 | D、△ABC内部 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在斜三棱柱ABC-A1B1C1中,∠A1AC=∠ACB=
如图所示,在斜三棱柱ABC-A1B1C1中,∠A1AC=∠ACB=| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.

(1)若D是BC的中点.求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,
求证:截面MBC1⊥侧面BB1C1C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com