练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A处出发，经正方体的表面，按最短路线爬行到达顶点C1位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是（ ）
    A．①②
    B．①③
    C．②④
    D．③④
    【答案】分析：本题可把正方体沿着某条棱展开到一个平面成为一个矩形，连接此时的对角线AC1即为所求最短路线．
    解答：解：由点A经正方体的表面，按最短路线爬行到达顶点C1位置，共有6种展开方式，若把平面ABA1和平面BCC1展到同一个平面内，
    在矩形中连接AC1会经过BB1的中点，故此时的正视图为②．
    若把平面ABCD和平面CDD1C1展到同一个平面内，在矩形中连接AC1会经过CD的中点，此时正视图会是④．
    其它几种展开方式对应的正视图在题中没有出现或者已在②④中了，
    故选C
    点评：本题考查空间几何体的展开图与三视图，是一道基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

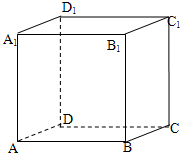
    ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2007段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•株洲模拟）已知ABCD-A1B1C1D1为单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每走完一条棱称为“走完一段”，白蚂蚁爬行的路线是AA1→A1D1→…，黑蚂蚁爬行的路线是AB→BB1→…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（其中i是自然数），设黑、白蚂蚁都走完2012段后各停止在正方体的某个顶点处，这时黑、白两只蚂蚁的距离是
    		2
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2007段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（　　）
    A．
    		2
    		B．1C．0D．
    		3
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年广东省广州六中高二（下）期中数学试卷（解析版） 题型：选择题

    ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2007段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（ ）

    A．
    B．1
    C．0
    D．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西大学附中高二（上）10月月考数学试卷（理科）（解析版） 题型：填空题

    已知ABCD-A1B1C1D1为单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每走完一条棱称为“走完一段”，白蚂蚁爬行的路线是AA1→A1D1→…，黑蚂蚁爬行的路线是AB→BB1→…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（其中i是自然数），设黑、白蚂蚁都走完2012段后各停止在正方体的某个顶点处，这时黑、白两只蚂蚁的距离是    ．

    查看答案和解析>>

    同步练习册答案