
【题目】如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区. 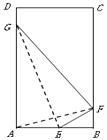
(1)请确定入口F的选址范围;
(2)设商业区的面积为S1 , 绿化区的面积为S2 , 商业区的环境舒适度指数为 ![]() ,则入口F如何选址可使得该商业区的环境舒适度指数最大?
,则入口F如何选址可使得该商业区的环境舒适度指数最大?
【答案】
(1)解:以A为原点,AB所在直线为x轴,建立如图所示平面直角坐标系,
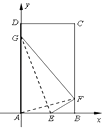
则A(0,0),
设F(2,2a)(0<2a<4),则AF的中点为(1,a),斜率为a,
而EG⊥AF,故EG的斜率为 ![]() ,
,
则EG的方程为 ![]() ,
,
令x=0,得 ![]() ;
;
令y=0,得 ![]() ;
;
由 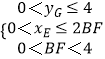 ,得
,得 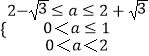 ,
,
∴ ![]() ,
,
即入口F的选址需满足BF的长度范围是 ![]() (单位:km)
(单位:km)
(2)解:因为 ![]() ,
,
故该商业区的环境舒适度指数 ![]() ,
,
所以要使 ![]() 最大,只需S1最小.
最大,只需S1最小.
设 ![]() ,
,
则 ![]() ,
,
令f'(a)=0,得 ![]() 或
或 ![]() (舍),
(舍),
a,f'(a),f(a)的情况如下表:
a | 2﹣ | (2﹣ |
|
| 1 |
f'(a) | ﹣ | 0 | + | ||
f(a) | 减 | 极小 | 增 |
故当 ![]() ,即入口F满足
,即入口F满足 ![]() km时,该商业区的环境舒适度指数最大
km时,该商业区的环境舒适度指数最大
【解析】(1)以A为原点,AB所在直线为x轴,建立如图所示平面直角坐标系,则A(0,0),设F(2,2a)(0<2a<4),则AF的中点为(1,a),斜率为a,EG⊥AF,求出EG的方程,列出不等式即可求出;(2)因为 ![]() ,该商业区的环境舒适度指数
,该商业区的环境舒适度指数 ![]() ,所以要使
,所以要使 ![]() 最大,只需S1最小.转化为求其最小值.
最大,只需S1最小.转化为求其最小值.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
![]()
为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表2:
得到下表2:
![]()
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2010年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中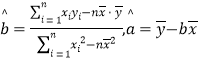 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,且A>0,ω>0,0<φ<π)的部分图象如图所示. 
(1)求A,ω,φ的值;
(2)设θ为锐角,且f(θ)=﹣ ![]() ,求f(θ﹣
,求f(θ﹣ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥D﹣ABC及其正视图和侧视图如右图所示,且顶点A,B,C,D均在球O的表面上,则球O的表面积为( ) 
A.32π
B.36π
C.128π
D.144π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= ![]() CC1 , 则异面直线A1E与AF所成角的余弦值为( )
CC1 , 则异面直线A1E与AF所成角的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,△BCD为正三角形,AD=AB=2, ![]() ,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°. 
(1)求证:平面PAC⊥平面PDB;
(2)求已知二面角A﹣PB﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com