
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(2)求所有的实数![]() ,使得对任意
,使得对任意![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的下方;
图象的下方;
(3)若存在![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() ;
;
【解析】
试题分析:(1) ,
,
由![]() 在
在![]() 上是增函数,则
上是增函数,则 ,即
,即![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.
(2)由题意得对任意的实数![]() ,
,![]() 恒成立,即
恒成立,即![]() ,当
,当![]() 恒成立,
恒成立,
即![]() ,得
,得![]() ,
,
故只要![]() 且
且![]() 在
在![]() 上恒成立即可,
上恒成立即可,
在![]() 时,只要
时,只要![]() 的最大值小于
的最大值小于![]() 且
且![]() 的最小值大于
的最小值大于![]() 即可,
即可,
而当![]() 时,
时, ,
,![]() 为增函数,
为增函数,![]() ;
;
当![]() 时,
时,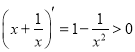 ,
,![]() 为增函数,
为增函数,![]() ,所以
,所以![]() .
.
(3)当![]() 时,
时,![]() 在
在![]() 上是增函数,则关于
上是增函数,则关于![]() 的方程
的方程![]() 不可能有三个不等的实数根;
不可能有三个不等的实数根;
则当![]() 时, 由
时, 由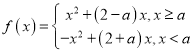 ,
,
得在![]() 时,
时,![]() 对称轴
对称轴![]() ,则
,则![]() 在
在![]() 为增函数,
为增函数,
此时![]() 的值域为
的值域为![]() ,
,
在![]() 时,
时,![]() 对称轴
对称轴![]() ,则
,则![]() 在
在![]() 为增函数,
为增函数,
此时![]() 的值域为
的值域为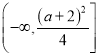 ,
,![]() 在
在![]() 为减函数,此时
为减函数,此时![]() 的值域为
的值域为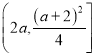 ;
;
由存在![]() ,方程
,方程![]() 有三个不相等的实根,则
有三个不相等的实根,则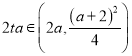 ,
,
即存在![]() ,使得
,使得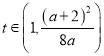 即可,令
即可,令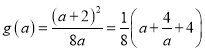 ,
,
只要使![]() 即可,而
即可,而![]() 在
在![]() 上是增函数,
上是增函数,![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() ;
;
同理可求当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ;
;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() 两点,若
两点,若![]() 恰好为线段的三等分点,求直线
恰好为线段的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府调查了工薪阶层![]() 人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是
人的月工资收人,并根据调查结果画出如图所示的频率分布直方图,其中工资收人分组区间是![]() .(单位:百元)
.(单位:百元)

(1)为了了解工薪阶层对工资收人的满意程度,要用分层抽样的方法从调查的![]() 人中抽取
人中抽取![]() 人做电话询问,求月工资收人在
人做电话询问,求月工资收人在![]() 内应抽取的人数;
内应抽取的人数;
(2)根据频率分布直方图估计这![]() 人的平均月工资为多少元.
人的平均月工资为多少元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
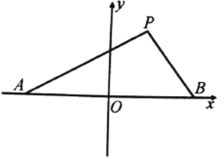
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 是轨迹为
是轨迹为![]() 上不同于
上不同于![]() 的两点,且满足
的两点,且满足![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某农科所记录了5组昼夜温差与100颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求出线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是第1组与第5组的两组数据,请根据第2组至第4组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: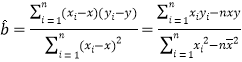 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() ,
,![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设函数![]() 有两个极值点
有两个极值点![]() ,
,![]() 且
且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com