
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
分析 由题意可得函数的图象关于直线x=$\frac{π}{4}$ 对称,再根据f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上有最小值、无最大值,可得ω$\frac{π}{4}$+$\frac{π}{6}$=$\frac{3π}{2}$,由此求得ω的值.
解答 解:对于函数f(x)=sin(ωx+$\frac{π}{6}$),由f($\frac{π}{6}$)=f($\frac{π}{3}$),可得函数的图象关于直线x=$\frac{\frac{π}{6}+\frac{π}{3}}{2}$=$\frac{π}{4}$ 对称,
再根据f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上有最小值、无最大值,可得ω•$\frac{π}{4}$+$\frac{π}{6}$=$\frac{3π}{2}$,求得ω=$\frac{16}{3}$,
故选:C.
点评 本题主要考查正弦函数的图象的对称性,函数的最值,属于基础题.


科目:高中数学 来源: 题型:选择题
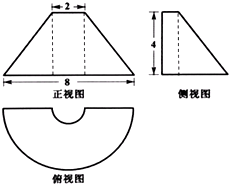 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )| A. | 12+$\frac{47π}{2}$ | B. | 12+23π | C. | 12+24π | D. | 12+$\frac{45}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
| A. | 7 | B. | 8.5 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com