
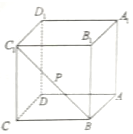
 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:分析 对于①:容易证明AD1∥BC1,从而BC1∥平面AD1C,以P为顶点,平面AD1C为底面,易得;
对于②:可以从向量的角度进行判断;
对于③:平面PD1A平面ACD1的法向量的夹角是不变的,得到结论;
对于④:根据异面直线的判定定理,可得结论;
对于⑤:点M到点D和C1距离相等,故点M在平面A1D1CB上,进而可得结论.
解答 解:对于①:容易证明AD1∥BC1,从而BC1∥平面AD1C,
故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,
则三棱锥A-D1PC的体积不变;①正确;
对于②:∵随着P点的移动,$\overrightarrow{AP}$与平面ACD1的法向量的夹角也是变化的,∴②错误
对于③:∵平面PD1A平面ACD1的法向量的夹角是不变的,∴③正确;
对于④:AD∥平面B1C1CB,B1P?平面B1C1CB,B1P与AD不平行,故直线AD与直线B1P为异面直线;④正确;
对于⑤,点M到点D和C1距离相等,故点M在平面A1D1CB上,又由M在平面A1B1C1D1上,故点M一定在直线A1D1上.故⑤正确.
故答案为:①③④⑤
点评 本题考查三棱锥体积求法中的等体积法;线面平行、垂直的判定,要注意使用转化的思想.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
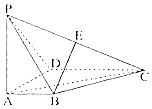 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{5}$ | B. | $3+\sqrt{5}$ | C. | $14+6\sqrt{5}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
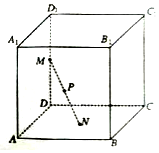 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32017-1 | B. | $\frac{{3}^{2017}-1}{2}$ | C. | 32017+1 | D. | $\frac{{3}^{2017}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com