
【题目】在平面直角坐标系中,已知圆![]() 过以下4个不同的点:
过以下4个不同的点:![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)先将圆![]() 向左平移
向左平移![]() 个单位后,再将所有点的横坐标、纵坐标都伸长到原来的
个单位后,再将所有点的横坐标、纵坐标都伸长到原来的![]() 倍得到圆
倍得到圆![]() ,若
,若![]() 两个点分别在直线
两个点分别在直线![]() 和
和![]() 上,
上,![]() 为圆
为圆![]() 上任意一点,且
上任意一点,且![]() (
(![]() 为常数),证明直线
为常数),证明直线![]() 过圆
过圆![]() 的圆心,并求
的圆心,并求![]() 的值.
的值.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对该班40名学生进行了问卷调查,得到了如下的![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
喜爱打篮球 | 19 | 15 | 34 |
不喜爱打篮球 | 1 | 5 | 6 |
总计 | 20 | 20 | 40 |
(1)在女生的20个个体中,随机抽取2人,记随机变量![]() 为抽到“不喜爱篮球”的人数,求
为抽到“不喜爱篮球”的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)判断能否在犯错误的概率不超过0.1的条件下认为喜爱篮球与性别有关?
附: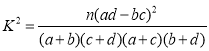 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com