
分析 延长BG于E,使得BG=GE,BE交AC于D,连接EC,利用S△ABC=S△ABG+S△BCE,可求△ABC的面积.
解答 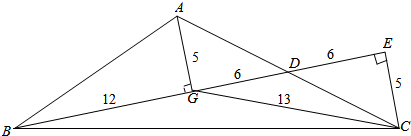 解:延长BG于E,使得BG=GE,BE交AC于D
解:延长BG于E,使得BG=GE,BE交AC于D
∵BG=2GD
∴GD=6
∵GE=BG=12
∴DE=6,GD=DE
连接EC,
∵D是AC的中点,AD=CD,且∠ADG=∠CDE
∴△AGD≌△CED(SAS),即S△AGD=S△CED,
∴EC=AG=5
∵CE=5,GE=12,CG=13
∴CE2+GE2=CG2
∴∠GEC=90°
∴∠AGB=90°
又∵AG=5,BG=12
∴S△ABC=S△ABG+S△BCE=$\frac{1}{2}$×AG×BG+$\frac{1}{2}$×CE×BE=$\frac{1}{2}$×5×12+$\frac{1}{2}$×5×24=90
点评 本题考查求△ABC的面积,考查学生的计算能力,正确转化是关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com