
 如图所示,已知D是面积为1的△ABC的边AB上任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设
如图所示,已知D是面积为1的△ABC的边AB上任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| 1 |
| 2 |
| a+b+c |
| 3 |
| S△ADE |
| S△ABC |
| ||
|
| λ1AB•λ2AC |
| AB•AC |
| h1 |
| h2 |
| DB |
| DA |
| 1-λ1 |
| λ1 |
| S△DBF |
| S△ADE |
| ||
|
| 1-λ1 |
| λ1 |
| S△ADE |
| S△ABC |
| ||
|
| h1 |
| h2 |
| DB |
| DA |
| 1-λ1 |
| λ1 |
| S△DBF |
| S△ADE |
| ||
|
| 1-λ1 |
| λ1 |
| λ3(1-λ1) |
| λ1 |
| λ2+ λ3+1-λ1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |



 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
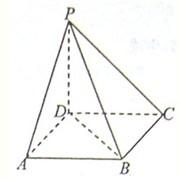 如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD.
如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知正四棱锥S—ABCD侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60°
C.45° D.30°
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三一轮复习质量检测理科数学 题型:选择题
如图所示,已知正四棱锥S—ABCD侧棱长为 ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
A.90° B.60° C.45° D.30°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com