
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x. 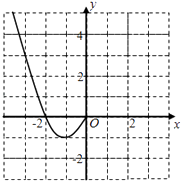
(1)现已画出函数f(x)在y轴左侧的图像,如图所示,请补出完整函数f(x)的图像,并根据图像写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
【答案】
(1)解:因为函数为偶函数,故图像关于y轴对称,补出完整函数图像如图:
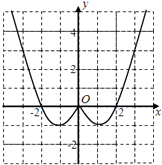
所以f(x)的递增区间是(﹣1,0),(1,+∞)
(2)解:设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以x>0时,f(x)=x2﹣2x,
故f(x)的解析式为 ![]()
值域为{y|y≥﹣1}
【解析】(1)因为函数为偶函数,故图像关于y轴对称,由此补出完整函数f(x)的图像即可,再由图像直接可写出f(x)的增区间.(2)可由图像利用待定系数法求出x>0时的解析式,也可利用偶函数求解析式,值域可从图形直接观察得到.
【考点精析】掌握函数的值域和函数的单调性是解答本题的根本,需要知道求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )将
)将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0.
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
(3)设该方程的两个实数根分别为x1 , x2 , 若2(x1+x2)+x1x2+10=0,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
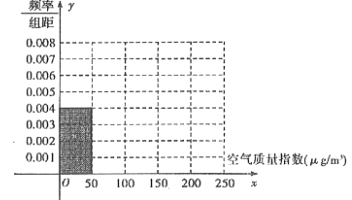
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={x|3≤x<9},B={x|1<x<7},C={x|x>m}.
(1)求A∪B;
(2)求(RA)∩B;
(3)若BC,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com