
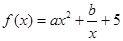
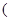 常数
常数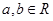 )满足
)满足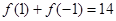 .
.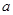 的值,并就常数
的值,并就常数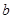 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性; 在区间
在区间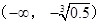 上单调递减,求
上单调递减,求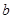 的最小值;
的最小值;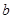 取最小值时,证明:
取最小值时,证明: 恰有一个零点
恰有一个零点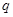 且存在递增的正整数数列
且存在递增的正整数数列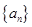 ,使得
,使得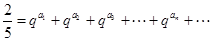 成立.
成立. ,
, 时是偶函数,
时是偶函数, 时,非奇非偶函数;(2)
时,非奇非偶函数;(2) ;(3)证明见解析.
;(3)证明见解析. 可求得
可求得 ,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即
,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即 或
或 ;(2)据题意,即当
;(2)据题意,即当 时,总有
时,总有 成立,变形整理可得
成立,变形整理可得 ,由于分母
,由于分母 ,故
,故 ,即
,即 ,注意到
,注意到 ,
, ,从而
,从而 ,因此有
,因此有 ;(3)在(2)的条件下,
;(3)在(2)的条件下, ,理论上讲应用求出零点
,理论上讲应用求出零点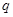 ,由函数表达式可看出,当
,由函数表达式可看出,当 时,无零点,当
时,无零点,当 时,函数
时,函数 是递增函数,如有零点,只有一个,解方程
是递增函数,如有零点,只有一个,解方程 ,即
,即 ,根据零点存在定理确定出
,根据零点存在定理确定出 ,这个三次方程具体的解求不出,但可变形为
,这个三次方程具体的解求不出,但可变形为 ,想到无穷递缩等比数列的和,有
,想到无穷递缩等比数列的和,有 ,因此可取
,因此可取 .证毕.
.证毕.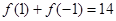 得
得 ,解得
,解得 .
. ,定义域为
,定义域为
 时,对于定义域内的任意
时,对于定义域内的任意 ,有
,有 ,
, 为偶函数 2分
为偶函数 2分 时,
时, 从而
从而 ,
, 不是奇函数;
不是奇函数; ,
, 不是偶函数,
不是偶函数, 非奇非偶. 4分
非奇非偶. 4分 ,总有
,总有 恒成立,即
恒成立,即 ,得
,得 . 6分
. 6分
 ,
, ,
, ,从而
,从而 .
. ,∴
,∴ ,
,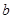 的最小值等于
的最小值等于 . 10分
. 10分 .
. 时,
时, 恒成立,函数
恒成立,函数 在
在 无零点. 12分
无零点. 12分 时,对于任意的
时,对于任意的 ,恒有
,恒有 ,
, ,所以函数
,所以函数 在
在 上递增,又
上递增,又 ,
, ,
,
 在
在 是有一个零点
是有一个零点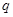 .
. 恰有一个零点
恰有一个零点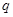 ,且
,且 15分
15分 ,得
,得 ,
, ,故
,故 ,
, 18分
18分

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 与g(x)=
与g(x)= ,表示同一个函数.
,表示同一个函数.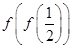 =0.
=0.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上的一个映射,正整数数对
上的一个映射,正整数数对 在映射f下的象为实数z,记作
在映射f下的象为实数z,记作 . 对于任意的正整数
. 对于任意的正整数 ,映射
,映射 由下表给出:
由下表给出: |  |  |  |
 |  |  |  |
 __________,使不等式
__________,使不等式 成立的x的集合是_____________.
成立的x的集合是_____________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,均有
,均有 成立,则称函数
成立,则称函数 在定义域
在定义域 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为()
的最小值为()| A.4 | B.3 | C.1 | D.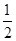 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在区间
在区间 上的导函数为
上的导函数为 ,
, 在区间
在区间 上的导函数为
上的导函数为 ,若在区间
,若在区间 上
上 恒成立,则称函数
恒成立,则称函数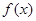 在区间
在区间 上为“凸函数”.已知
上为“凸函数”.已知 ,若对任意的实数
,若对任意的实数 满足
满足 时,函数
时,函数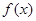 在区间上
在区间上 为“凸函数”,则
为“凸函数”,则 的最大值为( )
的最大值为( )| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com