
分析 由分段函数可先求f(4)=-1,再求f(-1);考虑当x≥0时,x<0时,f(x)的单调性,求得范围,即可得到最值.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1-\sqrt{x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,可得
f(4)=1-$\sqrt{4}$=-1,
f(f(4))=f(-1)=2-1=$\frac{1}{2}$,
当x≥0时,f(x)=1-$\sqrt{x}$递减,即有f(x)≤1;
当x<0时,f(x)=2x∈(0,1).
综上可得x=0时,取得最大值1.
故答案为:$\frac{1}{2}$,1.
点评 本题考查分段函数的运用:求函数值,同时考查函数的最值的求法,注意运用单调性,属于中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
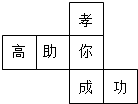 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{5}{3}$ ) | B. | [0,$\frac{5}{3}$] | C. | [1,$\frac{5}{3}$ ) | D. | [1,$\frac{5}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com