
【题目】设函数f(x)=mlnx(m∈R),g(x)=cosx.
(1)若函数 ![]() 在(1,+∞)上单调递增,求m的取值范围;
在(1,+∞)上单调递增,求m的取值范围;
(2)设函数φ(x)=f(x)+g(x),若对任意的 ![]() ,都有φ(x)≥0,求m的取值范围;
,都有φ(x)≥0,求m的取值范围;
(3)设m>0,点P(x0 , y0)是函数f(x)与g(x)的一个交点,且函数f(x)与g(x)在点P处的切线互相垂直,求证:存在唯一的x0满足题意,且 ![]() .
.
【答案】
(1)解:由题意,知 ![]() ,所以
,所以 ![]() .
.
由题意, ![]() ,即
,即 ![]() 对x∈(1,+∞)恒成立.
对x∈(1,+∞)恒成立.
又当x∈(1,+∞)时, ![]() ,所以m≥1
,所以m≥1
(2)解:因为φ(x)=f(x)+g(x)=mlnx+cosx,所以 ![]() .
.
①当m≤0时,因为 ![]() ,所以lnx>0,cosx<0,故φ(x)<0,不合题意.
,所以lnx>0,cosx<0,故φ(x)<0,不合题意.
②当m>0时,因为 ![]() ,所以φ'(x)>0,故φ(x)在
,所以φ'(x)>0,故φ(x)在 ![]() 上单调递增.
上单调递增.
欲φ(x)≥0对任意的 ![]() 都成立,则需φ(π)≥0,所以mlnπ+cosπ≥0,解得
都成立,则需φ(π)≥0,所以mlnπ+cosπ≥0,解得 ![]() .
.
综上所述,m的取值范围是 ![]()
(3)解:证明:因为 ![]() ,g'(x)=﹣sinx,且函数f(x)与g(x)在点P(x0,y0)处的切线互相垂直,
,g'(x)=﹣sinx,且函数f(x)与g(x)在点P(x0,y0)处的切线互相垂直,
所以 ![]() ,即msinx0=x0(*).
,即msinx0=x0(*).
又点P(x0,y0)是函数f(x)与g(x)的一个交点,所以mlnx0=cosx0(**).
由(*)(**)消去m,得x0lnx0﹣sinx0cosx0=0.
①当x0∈(0,1]时,因为m>0,所以mlnx0≤0,且cosx0>0,此与(**)式矛盾.
所以在(0,1]上没有x0适合题意
②当x0∈(1,+∞)时,设r(x)=xlnx﹣sinxcosx,x∈(1,+∞).
则r'(x)=lnx+1﹣cos2x>0,即函数r(x)在(1,+∞)上单调递增,
所以函数r(x)在(1,+∞)上至多有一个零点.
因为r(1)=ln1﹣sin1cos1=﹣sin1cos1<0, ![]() ,
,
且r(x)的图象在(1,+∞)上不间断,所以函数r(x)在 ![]() 有唯一零点.
有唯一零点.
即只有唯一的x0∈(1,+∞),使得x0lnx0﹣sinx0cosx0=0成立,且 ![]() .
.
综上所述,存在唯一的x0∈(0,+∞),且 ![]()
【解析】(1)根据求导研究函数的单调性令 h ' ( x ) ≥ 0,即得m的取值范围 。(2)利用求导函数讨论导函数正负进而得到函数的单调性。(3)利用求导函数以及函数f(x)与g(x)在点P处的切线互相垂直,得到msinx0=x0;又点P(x0,y0)是函数f(x)与g(x)的一个交点,得到mlnx0=cosx0,进而得到x0lnx0﹣sinx0cosx0=0.对x0分情况讨论,当x0∈(0,1]时,在(0,1]上没有x0适合题意。当x0∈(1,+∞)时函数r(x)在(1,+∞)上至多有一个零点,再根据零点定理可得,函数r(x)有唯一零点,即得结果。
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)写出直线l的普通方程与曲线C的直角坐标方程;
(Ⅱ)设曲线C经过伸缩变换 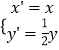 得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,﹣1)
,﹣1) ![]() =(
=( ![]() ),设函数f(x)=
),设函数f(x)= ![]() +1.
+1.
(1)求函数f(x)的单调递增区间;
(2)若关于x的方程f(x)=a在区间[0,π]上有实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}为递增的等差数列,a1=f(x+1),a2=0,a3=f(x﹣1),其中f(x)=x2﹣4x+2,则数列{an}的通项公式为( )
A.an=n﹣2
B.an=2n﹣4
C.an=3n﹣6
D.an=4n﹣8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c且a+2c=2bcosA.
(1)求角B的大小;
(2)若b=2 ![]() ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BOC中,OA,OB,OC两两垂直,点D,E分别为棱BC,AC的中点,F在棱AO上,且满足OF= ![]() ,已知OA=OC=4,OB=2.
,已知OA=OC=4,OB=2.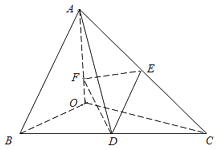
(1)求异面直线AD与OC所成角的余弦值;
(2)求二面角C﹣EF﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.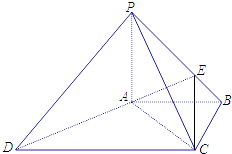
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com