
分析 原式变形为$\frac{\root{3}{3}-\root{3}{2}}{(\root{3}{3}-\root{3}{2})(\root{3}{{2}^{2}}+\root{3}{2}•\root{3}{3}+\root{3}{{3}^{2}})}$,再利用“立方差公式”即可得出.
解答 解:原式=$\frac{\root{3}{3}-\root{3}{2}}{(\root{3}{3}-\root{3}{2})(\root{3}{{2}^{2}}+\root{3}{2}•\root{3}{3}+\root{3}{{3}^{2}})}$=$\frac{\root{3}{3}-\root{3}{2}}{3-2}$=$\root{3}{3}-\root{3}{2}$.
故答案为:$\root{3}{3}-\root{3}{2}$.
点评 本题考查了乘法公式的应用、根式的运算性质,考查了推理能力与计算能力,属于基础题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
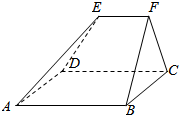 如图,在多面体ABCDEF中,已知面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
如图,在多面体ABCDEF中,已知面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com