
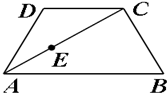
 如图,等腰梯形ABCD中,$\overrightarrow{AB}=2\overrightarrow{DC}$,3$\overrightarrow{AE}=2\overrightarrow{EC}$.一双曲线经过C,D,E三点,且以A,B为焦点,则该双曲线离心率是$\sqrt{7}$.
如图,等腰梯形ABCD中,$\overrightarrow{AB}=2\overrightarrow{DC}$,3$\overrightarrow{AE}=2\overrightarrow{EC}$.一双曲线经过C,D,E三点,且以A,B为焦点,则该双曲线离心率是$\sqrt{7}$. 分析 可设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,由题意可得|CD|=c,设C在第一象限,由x=$\frac{c}{2}$,代入双曲线的方程,可得C的坐标,再由条件得$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{EC}$,运用向量共线的坐标表示,求得E的坐标,代入双曲线的方程,由离心率公式计算即可得到所求值.
解答 解:可设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1.
由2c=|AB|=2|CD|,可得|CD|=c,
设C在第一象限,
由x=$\frac{c}{2}$,可得y=b$\sqrt{\frac{{c}^{2}}{4{a}^{2}}-1}$,
即有C($\frac{1}{2}$c,b$\sqrt{\frac{{c}^{2}}{4{a}^{2}}-1}$),
又设A(-c,0),3$\overrightarrow{AE}=2\overrightarrow{EC}$,
可得$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{EC}$,即有E($\frac{-c+\frac{2}{3}•\frac{c}{2}}{1+\frac{2}{3}}$,$\frac{b\sqrt{\frac{{c}^{2}}{4{a}^{2}}-1}}{1+\frac{2}{3}}$),
即为(-$\frac{2}{5}$c,$\frac{2}{5}$b$\sqrt{\frac{{c}^{2}}{4{a}^{2}}-1}$),
代入双曲线的方程,可得$\frac{4}{25}$•$\frac{{c}^{2}}{{a}^{2}}$-$\frac{4}{25}$($\frac{{c}^{2}}{4{a}^{2}}$-1)=1,
由e=$\frac{c}{a}$,可得4e2-e2=21,解得e=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查双曲线的离心率的求法,注意运用向量的坐标表示,点满足双曲线的方程,考查化简整理的运算能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
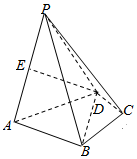 如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.
如图,在四棱锥P-ABCD中,△ABD是边长为2$\sqrt{3}$的正三角形,∠CBD=∠CDB=30°,E为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
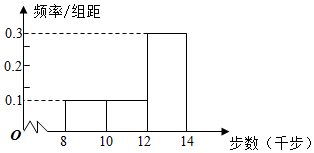 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com