
【题目】已知函数f(x)= ![]() sinxcosx+sin2x﹣
sinxcosx+sin2x﹣ ![]() .
.
(1)求f(x)的最小正周期及其对称轴方程;
(2)设函数g(x)=f( ![]() +
+ ![]() ),其中常数ω>0,|φ|<
),其中常数ω>0,|φ|< ![]() . (i)当ω=4,φ=
. (i)当ω=4,φ= ![]() 时,函数y=g(x)﹣4λf(x)在[
时,函数y=g(x)﹣4λf(x)在[ ![]() ,
, ![]() ]上的最大值为
]上的最大值为 ![]() ,求λ的值;
,求λ的值;
(ii)若函数g(x)的一个单调减区间内有一个零点﹣ ![]() ,且其图象过点A(
,且其图象过点A( ![]() ,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.
,1),记函数g(x)的最小正周期为T,试求T取最大值时函数g(x)的解析式.
【答案】
(1)解:函数f(x)= ![]() sinxcosx+sin2x﹣
sinxcosx+sin2x﹣ ![]() .
.
化简可得:f(x)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() )
)
f(x)的最小正周期T= ![]() ,
,
由2x﹣ ![]() =
= ![]() ,(k∈Z),可得对称轴方程为:x=
,(k∈Z),可得对称轴方程为:x= ![]() ,(k∈Z)
,(k∈Z)
(2)解:由函数g(x)=f( ![]() +
+ ![]() )=sin(ωx+φ),
)=sin(ωx+φ),
(i)当ω=4,φ= ![]() 时,函数y=g(x)﹣4λf(x)=sin(4x+
时,函数y=g(x)﹣4λf(x)=sin(4x+ ![]() )﹣4λsin(2x﹣
)﹣4λsin(2x﹣ ![]() )
)
=cos(4x﹣ ![]() )﹣4λsin(2x﹣
)﹣4λsin(2x﹣ ![]() )=1﹣2sin2(2x﹣
)=1﹣2sin2(2x﹣ ![]() )﹣4λsin(2x﹣
)﹣4λsin(2x﹣ ![]() )=﹣2[sin(2x﹣
)=﹣2[sin(2x﹣ ![]() )+λ]2+1+2λ2.
)+λ]2+1+2λ2.
∵x∈[ ![]() ,
, ![]() ]上,
]上,
则2x﹣ ![]() ∈[0,
∈[0, ![]() ].
].
故sin(2x﹣ ![]() )∈[0,1].
)∈[0,1].
当λ∈[﹣1,0]时,则有1+2λ2= ![]() ,解得:λ=-
,解得:λ=- ![]() ;
;
当λ∈(0,+∞)时,sin(2x﹣ ![]() )=0时,y取得最大值,此时﹣2[sin(2x﹣
)=0时,y取得最大值,此时﹣2[sin(2x﹣ ![]() )+λ]2+1+2λ2=1,与题意不符.
)+λ]2+1+2λ2=1,与题意不符.
当λ∈(﹣∞,﹣1)时,sin(2x﹣ ![]() )=1时,y取得最大值,此时﹣2[1+λ]2+1+2λ2=﹣1﹣4λ=
)=1时,y取得最大值,此时﹣2[1+λ]2+1+2λ2=﹣1﹣4λ= ![]() ,解得:λ=﹣
,解得:λ=﹣ ![]() ,不在其范围内,故舍去.
,不在其范围内,故舍去.
故得满足题意的λ的值为- ![]() .
.
(ii)函数g(x)=sin(ωx+φ),若函数的周期最大为T,单调减区间内有一个零点﹣ ![]() ,
,
且其图象过点A( ![]() ,1),则有
,1),则有 ![]() =
= ![]() =3π,解得:T=4π,∴ω=
=3π,解得:T=4π,∴ω= ![]() =
= ![]() .点(
.点( ![]() ,1)在图象上,可得:
,1)在图象上,可得: ![]() +φ=2kπ.∵|φ|<
+φ=2kπ.∵|φ|< ![]() .∴φ=﹣
.∴φ=﹣ ![]() 不符合题意.舍去.
不符合题意.舍去.
当 ![]() =
= ![]() =3π,解得:T=
=3π,解得:T= ![]() .∴ω=
.∴ω= ![]() .
.
点(- ![]() ,0)在图象上,
,0)在图象上, ![]() +φ=﹣π+2kπ.∵|φ|<
+φ=﹣π+2kπ.∵|φ|< ![]() .∴φ=
.∴φ= ![]() ,
,
∴g(x)的解析式为:g(x)=sin( ![]() x﹣
x﹣ ![]() )
)
点( ![]() ,1)在图象上,
,1)在图象上,
验证:sin( ![]() )=sin
)=sin ![]() =1符合题意.
=1符合题意.
故得g(x)的解析式为:g(x)=sin( ![]() x﹣
x﹣ ![]() )
)
【解析】(1)利用二倍角以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,结合三角函数的图象和性质对称轴方程;(2)(i)求出g(x)的解析式,当ω=4,φ= ![]() 时,求函数y=g(x)﹣4λf(x),化简,结合三角函数的图象和性质在[
时,求函数y=g(x)﹣4λf(x),化简,结合三角函数的图象和性质在[ ![]() ,
, ![]() ]上的最大值为
]上的最大值为 ![]() ,讨论,可求λ的值.(ii)若函数的周期最大为T,单调减区间内有一个零点﹣
,讨论,可求λ的值.(ii)若函数的周期最大为T,单调减区间内有一个零点﹣ ![]() ,且其图象过点A(
,且其图象过点A( ![]() ,1),则有
,1),则有 ![]() =
= ![]() =3π,求解T的最大值.可得ω;图象过点A(
=3π,求解T的最大值.可得ω;图象过点A( ![]() ,1),带入g(x)化简,求解φ,从而可得函数g(x)的解析式.
,1),带入g(x)化简,求解φ,从而可得函数g(x)的解析式.


科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)随机误差e是衡量预报精确度的一个量,它满足E(e)=0
(2)残差平方和越小的模型,拟合的效果越好;
(3)用相关指数R2来刻画回归的效果时,R2的值越小,说明模型拟合的效果越好;
(4)直线y=bx+a和各点(x1 , y1),(x2 , y2),…,(xn , yn)的偏差 ![]() 是该坐标平面上所有直线与这些点的偏差中最小的直线.
是该坐标平面上所有直线与这些点的偏差中最小的直线.
其中真命题的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某工程施工期间的将数量X(单位:mm)对工期的影响如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD. 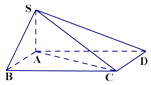
(1)证明:AC⊥平面SAB;
(2)若SA=2,求三棱锥A﹣SCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com