
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程;
(2)设![]() 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过![]() 作直线交椭圆于
作直线交椭圆于![]() 两点,求△
两点,求△![]() 的内切圆半径
的内切圆半径![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求椭圆标准方程,一般方法为待定系数法,即利用条件列出两个独立条件:一是离心率![]() ,二是根据点到直线距离公式得
,二是根据点到直线距离公式得 ,解得a2=3,b2=1,c2=2. (2)由等面积法得S△F1PQ=
,解得a2=3,b2=1,c2=2. (2)由等面积法得S△F1PQ=![]() (|PF1|+|F1Q|+|PQ|)·r=
(|PF1|+|F1Q|+|PQ|)·r=![]() |F1F2||y1-y2|,再由椭圆定义得ar=c|y1-y2|,,因此本题转化为求弦长,利用直线方程与椭圆方程方程组,结合韦达定理可得
|F1F2||y1-y2|,再由椭圆定义得ar=c|y1-y2|,,因此本题转化为求弦长,利用直线方程与椭圆方程方程组,结合韦达定理可得![]() ,最后利用变量分离结合基本不等式求最值
,最后利用变量分离结合基本不等式求最值
试题解析:(1)直线AB的方程为![]() ,即bx-ay-ab=0.
,即bx-ay-ab=0.
原点到直线AB的距离为 ,即3a2+3b2=4a2b2.①
,即3a2+3b2=4a2b2.①
![]() c2=
c2=![]() a2.②
a2.②
又a2=b2+c2,③
由①②③可得a2=3,b2=1,c2=2. 故椭圆的方程为![]() .
.
(2)F1(![]() ,0),F2(
,0),F2(![]() ,0),设P(x1,y1),Q(x2,y2).
,0),设P(x1,y1),Q(x2,y2).
由于直线PQ的斜率不为0,故设其方程为x=ky+![]() ,
,
联立直线与椭圆的方程,得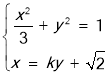 (k2+3)y2+2
(k2+3)y2+2![]() ky-1=0.
ky-1=0.
故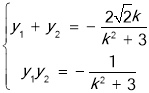 ④
④
而S△F1PQ=S△F1F2P![]() |F1F2||y1-y2|=
|F1F2||y1-y2|=![]() ,⑤
,⑤
将④代入⑤,得S△F1PQ=![]() .
.
又S△F1PQ=![]() (|PF1|+|F1Q|+|PQ|)·r=2a·r=2
(|PF1|+|F1Q|+|PQ|)·r=2a·r=2![]() r,
r,
所以![]() =2
=2![]() r,故r=
r,故r=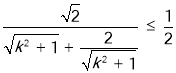 ,
,
当且仅当![]() ,即k=±1时,取得“=”.
,即k=±1时,取得“=”.
故△PQF1的内切圆半径r的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若直线l经过第二、三、四象限,则直线l的倾斜角的范围是 ( )
A. 0°≤α<90° B. 90°≤α<180°
C. 90°<α<180° D. 0°≤α<180°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】育才高中为了推进新课程改革,满足不同层次学生的需求,决定在每周的周一、周三、周五的课外活动期间同时开设“茶艺”、“模拟驾驶”、“机器人制作”、“数学与生活”和“生物与环境”选修课,每位有兴趣的同学可以在任何一天参加任何一门科目.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各选修课各天的满座的概率如下表:
生物与环境 | 数学与生活 | 机器人制作 | 模拟驾驶 | 茶艺 | |
周一 |
|
|
|
|
|
周三 |
|
|
|
|
|
周五 |
|
|
|
|
|
(1)求茶艺选修课在周一、周三、周五都不满座的概率;
(2)设周三各选修课中满座的科目数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的侧面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x<7},B={x|3<x<10},C={x|x<a}.
(1)求A∪B,(RA)∩B;
(2)若A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(﹣1,1)上的奇函数f(x),在x∈(﹣1,0)时,f(x)=2x+2﹣x.
(1)求f(x)在(﹣1,1)上的表达式;
(2)用定义证明f(x)在(﹣1,0)上是减函数;
(3)若对于x∈(0,1)上的每一个值,不等式m2xf(x)<4x﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若在区间![]() 上存在不相等的实数
上存在不相等的实数![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com