
分析 根据函数y的解析式,列出使解析式有意义的不等式组,求出解集即可.
解答 解:函数$y=ln(2sinx-\sqrt{2})+\sqrt{1-2cosx}$,
∴$\left\{\begin{array}{l}{2sinx-\sqrt{2}>0}\\{1-2cosx≥0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{sinx>\frac{\sqrt{2}}{2}}\\{cosx≤\frac{1}{2}}\end{array}\right.$,
即$\left\{\begin{array}{l}{\frac{π}{4}+2kπ<x<\frac{3π}{4}+2kπ,k∈Z}\\{\frac{π}{3}+2kπ≤x≤\frac{5π}{3}+2kπ,k∈Z}\end{array}\right.$,
即$\frac{π}{3}$+2kπ≤x<$\frac{3π}{4}$+2kπ,k∈Z;
∴y的定义域是$\{x|\frac{π}{3}+2kπ≤x<\frac{3π}{4}+2kπ,k∈Z\}$.
故答案为:{x|$\frac{π}{3}$+2kπ≤x<$\frac{3π}{4}$+2kπ,k∈Z}.
点评 本题考查了根据函数的解析式求定义域的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校同学设计了一个如图所示的“蝴蝶形图案”.其中AC,BD是过抛物线y=x2的两条相互垂直的弦(点A,B在第二象限),且AC,BD交于点$F({0,\frac{1}{4}})$,点E为y轴上的一点,记∠EFA=α,其中α为锐角:
某校同学设计了一个如图所示的“蝴蝶形图案”.其中AC,BD是过抛物线y=x2的两条相互垂直的弦(点A,B在第二象限),且AC,BD交于点$F({0,\frac{1}{4}})$,点E为y轴上的一点,记∠EFA=α,其中α为锐角:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
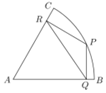 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com