
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 在
在![]() 的单调性;
的单调性;
(2)证明:![]()
![]() ,
,![]() ;
;
(3)设![]()
![]() ,对
,对![]() ,
,![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
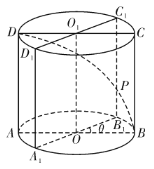
(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】疫情期间,有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
所用时间 | 10 | 11 | 12 | 13 |
通过公路1的频数 | 20 | 40 | 20 | 20 |
通过公路2的频数 | 10 | 40 | 40 | 10 |
(1)为进行某项研究,从所用时间为12的60辆汽车中随机抽取6辆,若用分层随机抽样的方法抽取,求从通过公路1和公路2的汽车中各抽取几辆:
(2)若从(1)的条件下抽取的6辆汽车中,再任意抽取2辆汽车,求这2辆汽车至少有1辆通过公路1的概率;
(3)假设汽车A只能在约定时间的前11h出发,汽车B只能在约定时间的前12h出发.为了尽最大可能在各自允许的时间内将货物从城市甲运到城市乙,汽车A和汽车B应如何选择各自的道路?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]()
![]() ,
,![]() ,
,![]() .
.
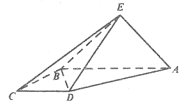
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰![]() 中,斜边
中,斜边![]() ,
,![]() 为直角边
为直角边![]() 上的一点,将
上的一点,将![]() 沿直线
沿直线![]() 折叠至
折叠至![]() 的位置,使得点
的位置,使得点![]() 在平面
在平面![]() 外,且点
外,且点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在线段
在线段![]() 上设
上设![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
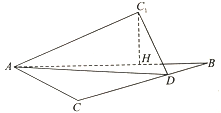
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com