
| A. | $\frac{5}{2}$ | B. | 8 | C. | $\frac{13}{2}$ | D. | $\frac{11}{2}$ |
分析 求出双曲线的焦点坐标,得出抛物线方程,设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MP|+|MD|取得最小,进而可推断出当D,M,P三点共线时|MP|+|MD|最小,答案可得.
解答 解:(4,6)代入双曲线C2:$\frac{x^2}{4}-\frac{y^2}{b^2}=1({b>0})$,可得$\frac{16}{4}-\frac{36}{{b}^{2}}=1$,∴b2=12,
∴c=4,∴F(4,0),
∵抛物线C1:y2=ax(a>0)的焦点与双曲线C2:$\frac{x^2}{4}-\frac{y^2}{b^2}=1({b>0})$的右焦点重合,
∴a=16,抛物线方程为y2=16x,
设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|,
∴要求|MP|+|MF|取得最小值,即求|MP|+|MD|取得最小,
当D,M,P三点共线时|MP|+|MD|最小,为4+4=8.
故选:B.
点评 本题考查双曲线的方程与性质,考查抛物线的定义、标准方程,以及简单性质的应用,判断当D,M,P三点共线时|PM|+|MD|最小,是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
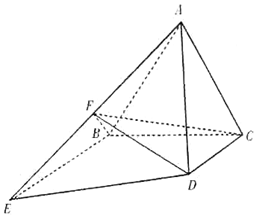 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -i | B. | i | C. | 1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
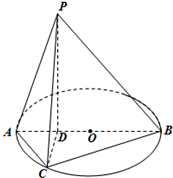 如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图,已知PD垂直于以AB为直径的圆O所在的平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com