
【题目】点F2是双曲线![]() 的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
A.8B.![]() C.9D.
C.9D.![]()
【答案】C
【解析】
由题意求出直线l1,l2的交点B为圆心在(0,﹣2),半径为1的圆,由双曲线的定义可得|AF2|=|AF1|+2a,所以|AB|+|AF2|=|AB|+|AF1|+6,当A,F1,B三点共线时,|AB|+|AF2|最小,过F1与圆心的直线与圆的交点B且在F1和圆心之间时最小.
由双曲线的方程可得a=3,b![]() ,焦点F(﹣2
,焦点F(﹣2![]() ,0),
,0),
可得|AF2|=|AF1|+2a=|AF1|+6,
所以|AB|+|AF2|=|AB|+|AF1|+6,
当A,F1,B三点共线时,|AB|+|AF2|最小,
联立直线l1,l2的方程![]() ,可得
,可得 ,消参数t可得x2+(y+2)2=1,
,消参数t可得x2+(y+2)2=1,
所以可得交点B的轨迹为圆心在![]() ,半径为1的圆,
,半径为1的圆,
所以|AB|+|AF2|=|AB|+|AF1|+6≥|BF1|+6≥|MF1|-1+6![]() 5=9,
5=9,
当过F1与圆心的直线与圆的交点B且在F1和圆心之间时最小.
所以|AB|+|AF2|的最小值为9,
故选:C



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),过线段
左侧),过线段![]() (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,设直线
处的切线平行,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
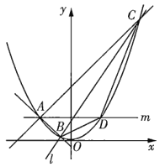
(1)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知边长为2的菱形ABCD,其中∠BAD=120°,AE∥CF,CF⊥平面ABCD,![]() ,
,![]() .
.
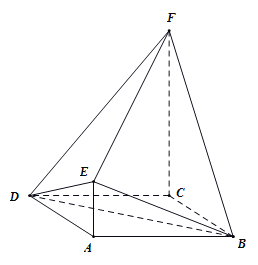
(1)求证:平面BDE⊥平面BDF;
(2)求二面角D﹣EF﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
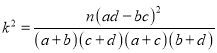
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD是边长为3的正方形,
的底面ABCD是边长为3的正方形,![]() 平面ABCD,
平面ABCD,![]() ,E为PD中点,过EB作平面
,E为PD中点,过EB作平面![]() 分别与线段PA、PC交于点M,N,且
分别与线段PA、PC交于点M,N,且![]() ,则
,则![]() ________;四边形EMBN的面积为________.
________;四边形EMBN的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com