【题目】给出下列两组数据：甲：12，13，11，10，14.乙：10，17，10，13，10.
（1）分别计算两组数据的平均差，并根据计算结果判断哪组数据波动大.
（2）分别计算两组数据的方差，并根据计算结果判断哪组数据波动大.
（3）以上两种判断方法的结果是否一致？
教材全解字词句篇系列答案科目：高中数学 来源： 题型：
【题目】设甲、乙、丙三个乒乓球协会分别选派3，1，2名运动员参加某次比赛，甲协会运动员编号分别为
，
，
，乙协会编号为
，丙协会编号分别为
，
，若从这6名运动员中随机抽取2名参加双打比赛.
（1）用所给编号列出所有可能抽取的结果；
（2）求丙协会至少有一名运动员参加双打比赛的概率；
（3）求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
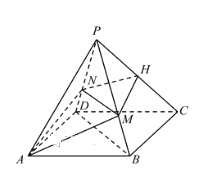
【题目】已知四棱锥
，底面
为菱形， 
为
上的点，过
的平面分别交
于点
，且
平面
．
（1）证明： 
；
（2）当
为
的中点， 
， 
与平面
所成的角为
，求平面AMHN与平面ABCD所成锐二面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面ABCD为平行四边形，PA⊥底面ABCD，
，
，
，
．
(1)求证：平面PCA⊥平面PCD；
(2)设E为侧棱PC上的一点，若直线BE与底面ABCD所成的角为45°，求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
（a＞b＞0）的两个焦点分别为F1，F2，离心率为
，过F1的直线l与椭圆C交于M，N两点，且△MNF2的周长为8．
（1）求椭圆C的方程；
（2）若直线y＝kx＋b与椭圆C分别交于A，B两点，且OA⊥OB，试问点O到直线AB的距离是否为定值，证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙、丙三人独立的对某一技术难题进行攻关。甲能攻克的概率为
，乙能攻克的概率为
，丙能攻克的概率为
；
（1）求这一技术难题被攻克的概率；
（2）若该技术难题未被攻克，上级不做任何奖励；若该技术难题被攻克，上级会奖励6万元。奖励规则如下：若只有一人攻克，则此人获得全部奖金6万元；若只有2人攻克，则此二人均分奖金，每人3万元；若三人均攻克，则每人2万元。在这一技术难题被攻克的前提下，设甲拿到的奖金数为
,求的分布列和数学期望。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“每天锻炼一小时，健康工作五十年，幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关，从单位随机抽取30名员工进行了问卷调查，得到了如下列联表：
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是
.
（1）请将上面的列联表补充完整（在答题卷上直接填写结果，不需要写求解过程），并据此资料分析能否有把握认为爱好运动与性别有关？
（2）若从这30人中的女性员工中随机抽取2人参加一活动，记爱好运动的人数为
，求的分布列、数学期望.参考数据：
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】曲线
，直线
关于直线
对称的直线为
，直线
，与曲线
分别交于点
、
和、
，记直线的斜率为
．
（Ⅰ）求证：
；
（Ⅱ）当
变化时，试问直线
是否恒过定点？若恒过定点，求出该定点坐标；若不恒过定点，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
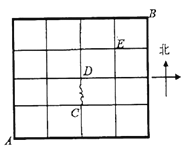
【题目】如图，某地有南北街道5条，东西街道5条，现在甲、乙、丙3名邮递员从该地西南角的邮局
出发，送信到东北角的
地，要求所走路程最短，设图中点
，
，
是交叉路口，且
路段由于修路不能通行.
（1）求甲从到共有多少种走法？（用数字作答）
（2）求甲经过点的概率；
（3）设3名邮递员恰有
名邮递员经过点，求随机变量的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
