
 的焦距为2,且过点
的焦距为2,且过点 ,已知F为椭圆的右焦点,A、B为椭圆上的两动点,直线l:x=2与x轴交于点G.
,已知F为椭圆的右焦点,A、B为椭圆上的两动点,直线l:x=2与x轴交于点G. ,c=1,从而b2=a2-c2=1,故可求椭圆的方程;
,c=1,从而b2=a2-c2=1,故可求椭圆的方程; ,计算原点O到直线x=my+2的距离为
,计算原点O到直线x=my+2的距离为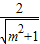 ,|AB|的长,表示出△AOB的面积,再换元,利用基本不等式求△AOB的面积最大,从而可求直线l'的方程.
,|AB|的长,表示出△AOB的面积,再换元,利用基本不等式求△AOB的面积最大,从而可求直线l'的方程. ,c=1,
,c=1, .
.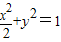 ,
, ,
, ,
, =
=
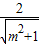 ,
,
 ≤
≤ ,当且仅当
,当且仅当 ,即t=4是等号成立,此时m2=6.
,即t=4是等号成立,此时m2=6. 时,△AOB面积最大,此时直线l的方程为
时,△AOB面积最大,此时直线l的方程为 .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:101网校同步练习 高二数学 苏教版(新课标·2004年初审) 苏教版 题型:013
椭圆![]() =1的焦距为2,则m的值等于
=1的焦距为2,则m的值等于
A.5或3
B.8
C.5
D.16
查看答案和解析>>
科目:高中数学 来源:新疆乌鲁木齐一中2012届高三第二次月考数学理科试题 题型:044
椭圆C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,已知F为椭圆的右焦点,A、B为椭圆上的两动点,直线l:x=2与x轴交于点G.
,已知F为椭圆的右焦点,A、B为椭圆上的两动点,直线l:x=2与x轴交于点G.
(1)求椭圆C的方程;
(2)若动点A、B、G三点共直线![]() ,试求当△AOB的面积最大时直线
,试求当△AOB的面积最大时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2013年山东省青岛市高考数学一模试卷(理科)(解析版) 题型:解答题
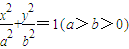 的焦距为
的焦距为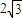 ,离心率为
,离心率为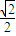 ,其右焦点为F,过点B(0,b)作直线交椭圆于另一点A.
,其右焦点为F,过点B(0,b)作直线交椭圆于另一点A.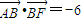 ,求△ABF外接圆的方程;
,求△ABF外接圆的方程; 相交于两点G、H,设P为N上一点,且满足
相交于两点G、H,设P为N上一点,且满足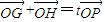 (O为坐标原点),当
(O为坐标原点),当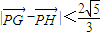 时,求实数t的取值范围.
时,求实数t的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com