
分析 (1)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;
(2)先化简函数g(x),根据g(x)的导数,判断函数g(x)的单调性,结合函数单调性和不等式之间的关系进行证明即可.
解答 解:(1)f(x)=x3-mx,f′(x)=3x2-m,
m≤0时,f′(x)≥0恒成立,f(x)在R递增,
m>0时,令f′(x)>0,解得:x>$\sqrt{\frac{m}{3}}$或x<-$\sqrt{\frac{m}{3}}$,令f′(x)<0,解得:-$\sqrt{\frac{m}{3}}$<x<$\sqrt{\frac{m}{3}}$,
∴f(x)在(-∞,-$\sqrt{\frac{m}{3}}$)递增,在(-$\sqrt{\frac{m}{3}}$,$\sqrt{\frac{m}{3}}$)递减,在($\sqrt{\frac{m}{3}}$,+∞)递增;
(2)m=1时,g(x)=$\frac{a{x}^{2}+ax}{f(x)}$+lnx=lnx+$\frac{a}{x-1}$,(x>0),
g′(x)=$\frac{1}{x}$-$\frac{a}{{(x-1)}^{2}}$=$\frac{{x}^{2}-(a+2)x+1}{{x(x-1)}^{2}}$,
∵函数g(x)在(0,$\frac{1}{e}$)内有极值,
∴g′(x)=0在(0,$\frac{1}{e}$)内有解,令h(x)=x2-(a+2)x+1=(x-α)(x-β),
∵αβ=1,不妨设0<α<$\frac{1}{e}$,则β>e,
由g′(x)>0,可得0<x<α或x>β;由g′(x)<0,可得α<x<1或1<x<β,
∴g(x)在(0,α)内递增,在(α,1)内递减,在(1,β)内递减,在(β,+∞)递增,
由s∈(0,1),可得g(s)≤g(α)=lnα+$\frac{a}{α-1}$,
由t∈(1,+∞),可得g(t)≥g(β)=lnβ+$\frac{a}{β-1}$,
∴g(t)-g(s)≥g(β)-g(α)
∵αβ=1,α+β=a+2
∴g(β)-g(α )=2lnβ+a×$\frac{α-β}{(β-1)(α-1)}$=2lnβ+β-$\frac{1}{β}$,
记h(β)=2lnβ+β-$\frac{1}{β}$(β>e)
则h′(β)=$\frac{2}{β}$+1+$\frac{1}{{β}^{2}}$>0,h(β)在(0,+∞)上单调递增
∴h(β)>h(e)=e+2-$\frac{1}{e}$,
∴g(t)-g(s)>e+2-$\frac{1}{e}$.
点评 本题以函数为载体,考查导数知识的运用,考查函数的极值与单调性,考查不等式的证明,综合性比较强.难度较大.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10.5 | 11 |
| 销售量y | 11 | 10 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | mf(xn)>nf(xm) | B. | mf(xn)<nf(xm) | ||
| C. | mf(xn)=nf(xm) | D. | mf(xn)与nf(xm)大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
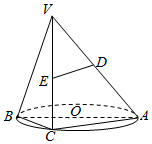 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com