
【题目】在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点. 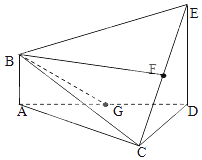
(1)证明:BF∥平面ACD;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(3)求点G到平面BCE的距离.
【答案】
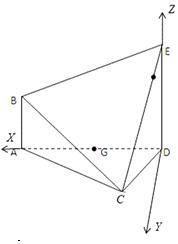
(1)证明:以D点为原点建立如图所示的空间直角坐标系,
使得x轴和z轴的正半轴分别经过点A和点E,则各点的坐标为D(0,0,0),B(2,0,1),E(0,0,2),C(1, ![]() ,0),F(
,0),F( ![]() ,
, ![]() ,1),
,1),
∴ ![]() =(
=( ![]() ,
, ![]() ,0)
,0)
又∵ ![]() =(0,0,2)为平面ACD的一个法向量
=(0,0,2)为平面ACD的一个法向量
且 ![]()
![]() =0
=0
∴BF∥平面ACD
(2)解:设平面BCE的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() ⊥
⊥ ![]() ,且
,且 ![]() ⊥
⊥ ![]() ,
,
由 ![]() =(1,
=(1, ![]() ,1),
,1), ![]() =(﹣1,
=(﹣1, ![]() ,2)得
,2)得 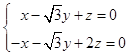 ,
,
不妨设y= ![]() ,则
,则 ![]() =(1,
=(1, ![]() ,2)
,2)
又∵ ![]() =(0,0,2)为平面ACD的一个法向量
=(0,0,2)为平面ACD的一个法向量
∴所求角θ满足cosθ= ![]()
∴平面BCE与平面ACD所成锐二面角的大小为 ![]()
(3)解:由已知G点坐标为(1,0,0),
∴ ![]() =(﹣1,0,﹣1),
=(﹣1,0,﹣1),
由(2)平面BCE的法向量为 ![]() =(1,
=(1, ![]() ,2)
,2)
∴所求距离d=| ![]() |=
|= ![]() .
.
【解析】(1)建立空间坐标系,求出直线BF的方向向量和平面ACD的法向量,根据两个向量垂直可得线面平行;(2)分别求出平面BCD与平面ACD的法向量,代入向量夹角公式,求出两个向量夹角的余弦值,进而可得二面角的大小(3)求出BG的方向向量的坐标,进而根据公式可得点G到平面BCE的距离.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,△ABC为等边三角形,PA=PB=PC=2,PA⊥PB,三棱锥P﹣ABC的外接球的表面积为( )
A.48π
B.12π
C.4 ![]() π
π
D.32 ![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在40分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上为优分(含80分),请你根据已知条件作出2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2﹣ax,a∈R
(1)若f(x)在P(x0 , y0)(x∈[ ![]() ))处的切线方程为y=﹣2,求实数a的值;
))处的切线方程为y=﹣2,求实数a的值;
(2)若x1 , x2(x1<x2)是函数f(x)的两个零点,f′(x)是函数f(x)的导函数,证明:f′( ![]() )<0.
)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=2时,求不等式f(x)<g(x)的解集;
(2)设a> ![]() ,且当x∈[
,且当x∈[ ![]() ,a]时,f(x)≤g(x),求a的取值范围.
,a]时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)在[0,+∞)单调递增,则使得f(x)>f(2x﹣1)成立的x的取值范围是( )
A.( ![]() ,1)
,1)
B.(﹣∞, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别是角A、B、C的对边,向量 ![]() =(2sinB,2﹣cos2B),
=(2sinB,2﹣cos2B), ![]() =(2sin2(
=(2sin2( ![]() +
+ ![]() ),﹣1)且
),﹣1)且 ![]() ⊥
⊥ ![]() .
.
(1)求角B的大小;
(2)若a= ![]() ,b=1,求c的值.
,b=1,求c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com