
【题目】一袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
【答案】(1)5;(2)答案见解析.
【解析】试题分析:(1)设黑球的个数为x,则白球的个数为10-x,记两个都是黑球得的事件为A,则至少有一个白球的事件与事件A为对立事件,由此能求出白球的个数;
(2)X服从超几何分布,其中N=10,M=5,n=3,其中P(X=k)=![]() ,k=0,1,2,3.
,k=0,1,2,3.
可求得分布列及数学期望.
试题解析:
(1)记“从袋中任意摸出2个球,至少得到1个白球”为事件A,
设袋中白球的个数为x,
则P(A)=1-![]() =
=![]() ,得到x=5.
,得到x=5.
(2)X服从超几何分布,其中N=10,M=5,n=3,其中P(X=k)=![]() ,k=0,1,2,3.
,k=0,1,2,3.
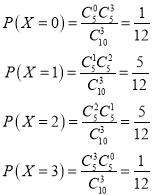
于是可得其分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望
E(X)=![]() ×0+
×0+![]() ×1+
×1+![]() ×2+
×2+![]() ×3=
×3=![]() .
.


科目:高中数学 来源: 题型:
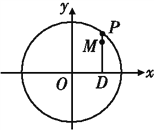
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1和l2的距离是![]() .
.
(1)求a的值.
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ?若能,求出P点坐标;若不能,请说明理由.
?若能,求出P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)具有较强的相关性,且两者之间有如下对应数据:
(单位:万元)具有较强的相关性,且两者之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中的线性回归方程,当广告费支出为10万元时,预测销售额是多少?
参考数据: ![]() ,
,![]() ,
,![]() 。
。
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 从
从![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() ,
, ![]() ,
, ![]() 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线![]() 的焦点,且椭圆
的焦点,且椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于
相交于![]() 两点.若线段
两点.若线段![]() 的中点的横坐标是
的中点的横坐标是![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时
(万元).当年产量不小于80千件时![]() (万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过分析,该工厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1、a2的等差中项,a2为b2、b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记![]() ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com