
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,讨论函数
时,讨论函数![]() 与
与![]() 的图象的交点个数.
的图象的交点个数.
【答案】(1) ![]() 时,增区间是
时,增区间是![]() ,无减区间;
,无减区间;![]() 时,增区间是
时,增区间是![]() ,减区间是
,减区间是![]() ;(2)1个.
;(2)1个.
【解析】
试题分析:(1)首先求得函数的定义与导函数,然后分![]() 、
、![]() 讨论函数的单调区间;(2)首先将问题为函数
讨论函数的单调区间;(2)首先将问题为函数![]() 的零点个数,然后分
的零点个数,然后分![]() 、
、![]() 、
、![]() 、
、![]() 求导研究函数的单调性,由此求得函数
求导研究函数的单调性,由此求得函数![]() 零点个数,从而使问题得解.
零点个数,从而使问题得解.
试题解析:(1) 函数![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() ,所以
,所以 ![]() 的增区间是
的增区间是![]() ,无减区间;
,无减区间;
当![]() 时,
时,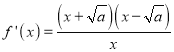 ,当
,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
综上,当![]() 时,函数
时,函数![]() 的增区间是
的增区间是![]() ,无减区间;当
,无减区间;当![]() 时,
时,![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(2)令![]() ,问题等价于求函数
,问题等价于求函数![]() 的零点个数.
的零点个数.
①当![]() 时,
时,![]() 有唯一零点;当
有唯一零点;当![]() 时,
时,![]() .
.
②当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取等号,所以
时取等号,所以![]() 为减函数.注意到
为减函数.注意到![]() ,所以
,所以![]() 在
在![]() 内有唯一零点;
内有唯一零点;
③当![]() 时,当
时,当![]() ,或
,或![]() 时,
时,![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
注意到![]() ,
,
所以![]() 在
在![]() 内有唯一零点;
内有唯一零点;
④当![]() 时,
时,![]() ,或
,或![]() 时,
时,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
注意到![]() ,
,
所以![]() 在
在![]() 内有唯一零点.
内有唯一零点.
综上,![]() 有唯一零点,即函数
有唯一零点,即函数![]() 与
与![]() 的图象有且仅有一个交点.
的图象有且仅有一个交点.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)对于函数![]() ,在定义域内给定区间
,在定义域内给定区间![]() ,如果存在
,如果存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是区间
是区间![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数![]() 是
是![]() 上的平均值函数,
上的平均值函数,![]() 就是它的均值点.现有函数
就是它的均值点.现有函数![]() 是区间
是区间![]() 上的平均值函数,求实数
上的平均值函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国男子篮球甲级联赛的规则规定:每场比赛胜者得2 分, 负者得1 分(每场比赛, 即使通过加时赛也必须分出胜负).某男篮甲级队实力强劲, 每场比赛获胜的概率为![]() 、失利的概率为
、失利的概率为![]() .求该队在赛程中间通过若干场比赛获得n 分的概率(设该队这一赛季的全部比赛场次数为S,这里0<n ≤S).
.求该队在赛程中间通过若干场比赛获得n 分的概率(设该队这一赛季的全部比赛场次数为S,这里0<n ≤S).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)若集合A={x|x2+5x﹣6=0},B={x|x2+2(m+1)x+m2﹣3=0}.
(1)若m=0,写出A∪B的子集;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 且x,
且x,![]() .
.
(1)判断![]() 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
(2)若不等式![]() 在
在![]() 上恒成立,试求实数a的取值范围;
上恒成立,试求实数a的取值范围;
(3)![]() 的值域为
的值域为![]() 函数
函数![]() 在
在![]() 上的最大值为M,最小值为m,若
上的最大值为M,最小值为m,若![]() 成立,求正数a的取值范围.
成立,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体 ABCD-A1B1C1D1 的棱长为 1 , E 、F 分别是棱 AB 、BC上的动点 ,且AE = BF .求直线 A1E 与C1F 所成角的最小值(用反三角函数表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com