
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
(1)见解析(2) ,
,
【解析】(1)连接AC,因为四边形ABCD是正方形,所以BD⊥AC.因为PA⊥平面ABCD,所以PA⊥BD.
又AC∩PA=A,所以BD⊥平面PAC.
又PC?平面PAC,所以PC⊥BD.
(2)解 ①设PA=x,三棱锥E-BCD的底面积为定值,在△PBC中,易知PB= ,PC=
,PC= ,
,
又BC=1,故△PBC直角三角形.又BE⊥PC,得EC= ,可求得该三棱锥的高h=
,可求得该三棱锥的高h= =
= .
.
当且仅当x= ,即x=
,即x= 时,三棱锥E-BCD的体积取到最大值,所以h=
时,三棱锥E-BCD的体积取到最大值,所以h= .
.
此时四棱锥E-ABCD的高为 .
.
②以点A为原点,AB,AD,AP所在直线为坐标轴建立空间直角坐标系,则A(0,0,0),C(1,1,0),D(0,1,0),P(0,0, ),易求得CE=
),易求得CE= CP.
CP.
所以 =
= +
+
 =
= ,
, =(0,1,0).
=(0,1,0).
设平面ADE的法向量n1=(x,y,z),则
即 ,令x=
,令x= ,则n1=(
,则n1=( ,0,-3),
,0,-3),
同理可得平面BDE的法向量n2= =(-1,-1,
=(-1,-1, ),所以cos〈n1,n2〉=
),所以cos〈n1,n2〉= =-
=- .所以sin〈n1,n2〉=
.所以sin〈n1,n2〉= .所以二面角A-DE-B的正弦值的大小为
.所以二面角A-DE-B的正弦值的大小为 .
.


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用2练习卷(解析版) 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:解答题
已知二次函数f(x)=ax2+bx+1(a>0),F(x)= 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.
(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用18练习卷(解析版) 题型:解答题
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).

(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:解答题
已知椭圆C的中心为平面直角坐标系xOy的原点,焦点在x轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆C的方程;
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的一点, =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:选择题
已知点O(0,0),A0(0,1),An(6,7),点A1,A2,…,An-1(n∈N,n≥2)是线段A0An的n等分点,则|  +
+ +…+OAn-1+
+…+OAn-1+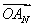 |等于( )
|等于( )
A.5n B.10n
C.5(n+1) D.10(n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com