
分析 (1)当m=3时,求出B={x|2≤x≤7},∁RB={x|x<2或x>7},即可求A∩∁RB;
(2)若A∪B=A,则B⊆A,分类讨论求m的取值范围..
解答 解:(1)由题意可知A={x|-2<x<5},
当 m=3 时,B={x|2≤x≤7},∁RB={x|x<2或x>7},
∴A∩∁RB={x|-2<x<2};
(2)∵A∪B=A,∴B⊆A.
①若B=∅,则m-1>2m+1,即m<-2;
②若B≠∅,$\left\{\begin{array}{l}{m-1≤2m+1}\\{m-1>-2}\\{2m+1<5}\end{array}\right.$,即-1<m<2,
综上,m 的取值范围是m<-2或-1<m<2.
点评 本题考查集合的运算,考查集合关系的运用,考查分类讨论的数学思想,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 210 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
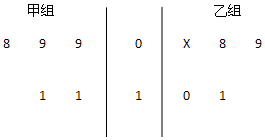 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
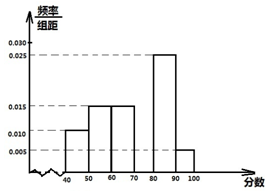 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com