练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （06年山东卷理）（12分）

    袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等。用ξ表示取出的3个小球上的最大数字，求：

    （1）取出的3个小球上的数字互不相同的概率；

    （2）随机变量ξ的概率分布和数学期望；

    （3）计分介于20分到40分之间的概率。

    解析：（I）解法一：“一次取出的3个小球上的数字互不相同”的事件记为，

    则

    解法二：“一次取出的3个小球上的数字互不相同的事件记为A”，“一次取出的3个小球上有两个数字相同”的事件记为，则事件和事件是互斥事件，因为

    所以.

    （II）由题意有可能的取值为：2，3，4，5.

    所以随机变量的概率分布为

    2

    3

    4

    5

     

    因此的数学期望为

    （Ⅲ）“一次取球所得计分介于20分到40分之间”的事件记为，则

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （06年山东卷理）设f(x)=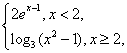  则不等式f(x)>2的解集为（   ）

    (A)（1，2）（3，+∞）                 (B)（，+∞）

    (C)（1，2） （ ，+∞）            (D)（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年山东卷理）在给定椭圆中，过焦点且垂直于长轴的弦长为，焦点到相应准线的距离为1，则该椭圆的离心率为（   ）

    (A)          (B)            (C)                   (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年山东卷理）下列四个命题中，真命题的序号有                  （写出所有真命题的序号）.

    ①将函数y=的图象按向量y=(-1,0)平移，得到的图象对应的函数表达式为y=

    ②圆x2+y2+4x-2y+1=0与直线y=相交，所得弦长为2

    ③若sin(+)=，sin(－)=,则tancot=5

    ④如图，已知正方体ABCD- A1B1C1D1，P为底面ABCD内一动点，P到平面AA1D1D的距离与到直线CC1的距离相等，则P点的轨迹是抛物线的一部分.

    （16题图）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年山东卷理）（12分）

    双曲线C与椭圆有相同的焦点，直线为C的一条渐近线。

    （1）求双曲线C的方程；

    （2）过点的直线，交双曲线C于A、B两点，交轴于Q点（Q点与C的顶点不重合），当，且时，求点的坐标。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年山东卷理）若         .

    查看答案和解析>>

    同步练习册答案