证明:(1)∵sinθ与cosθ的等差中项是sinx,等比中项是siny,
∴sinθ+cosθ=2sinx①,sinθcosθ=sin
2y②,
①
2-②×2,可得(sinθ+cosθ)
2-2sinθcosθ=4sin
2x-2sin
2y,即4sin
2x-2sin
2y=1.
∴4×

-2×
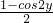
=1,即2-2cos2x-(1-cos2y)=1.
故证得cos2x=

cos2y;
(2)要证
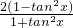
=
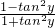
,只需证
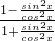
=
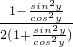
,
即证
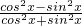
=

,即证cos
2x-sin
2x=

(cos
2y-sin
2y),只需证cos2x=

cos2y.
由(1)的结论,cos2x=

cos2y显然成立.
所以
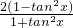
=
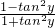
.
分析:(1)根据等差数列的性质可得2sinx等于sinθ+cosθ,记作①,根据等比数列的性质可得sin
2y等于sinθcosθ,记作②,然后①
2-②×2,利用同角三角函数间的基本关系化简,然后利用二倍角的正弦函数公式化简可得证;
(2)由(1)得到的结论,利用二倍角的余弦函数公式化简后,把分母看作“1”即为正弦与余弦函数的平方和,然后利用同角三角函数间的基本关系弦化切即可得证.
点评:此题考查学生灵活运用同角三角函数间的基本关系,以及二倍角的正弦、余弦函数公式化简求值,是一道综合题.学生在证明第二问时应注意“1”的灵活变换.

 (k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项.
(k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项. cos2y;(2)
cos2y;(2)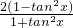 =
=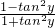 .
. -2×
-2×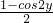 =1,即2-2cos2x-(1-cos2y)=1.
=1,即2-2cos2x-(1-cos2y)=1. cos2y;
cos2y;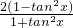 =
=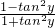 ,只需证
,只需证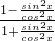 =
=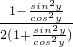 ,
,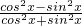 =
= ,即证cos2x-sin2x=
,即证cos2x-sin2x= (cos2y-sin2y),只需证cos2x=
(cos2y-sin2y),只需证cos2x= cos2y.
cos2y. cos2y显然成立.
cos2y显然成立.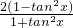 =
=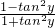 .
.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案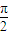 (k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项.
(k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项. cos2y;(2)
cos2y;(2)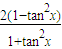 =
=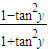 .
.