
����Ŀ����֪����������������������Ҫָ���������ָ��RO.��ָ���ǣ�����Ȼ����£�û���������룬ͬʱ�����˶�û������������һ����Ⱦ��ij�ִ�Ⱦ�����ˣ���Ѽ�����Ⱦ�������˵�ƽ����.���ļ��㹫ʽ�ǣ�![]() ȷ�ϲ���������
ȷ�ϲ���������![]() ϵ�м��������ϵ�м����ָ��һ���������У��������������ļ��ʱ�䣨��λ���죩.����ͳ�ƣ�ȷ�ϲ�����ƽ��������Ϊ
ϵ�м��������ϵ�м����ָ��һ���������У��������������ļ��ʱ�䣨��λ���죩.����ͳ�ƣ�ȷ�ϲ�����ƽ��������Ϊ![]() ���������������ļ��ʱ���ƽ����Ϊ
���������������ļ��ʱ���ƽ����Ϊ![]() �죬��������RO���ݼ��㣬�������ִ�Ⱦ������
�죬��������RO���ݼ��㣬�������ִ�Ⱦ������![]() �ִ������ɼ�����ĵò���������ԼΪ�� ��
�ִ������ɼ�����ĵò���������ԼΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������a��0��ʹ�ú���f��x����6a2lnx+4ax��g��x����x2��b����������ͼ��Ĺ����㴦��������ͬ����b�����ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �Ľ���Ϊ2�����ҽ���Ͷ���һ���˵��ֱ�ߵ�б��Ϊ
�Ľ���Ϊ2�����ҽ���Ͷ���һ���˵��ֱ�ߵ�б��Ϊ![]() ��
��![]() Ϊ����ԭ�㣮
Ϊ����ԭ�㣮
��������Բ![]() �ķ��̣�
�ķ��̣�
������б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ��������ֵΪ
��������ֵΪ![]() ��֤����
��֤���� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ij��УȫУѧ�����Ķ���������������200��ѧ��ÿ���Ķ�ʱ��![]() ����λ��Сʱ����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
����λ��Сʱ����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
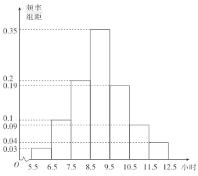
��1������200��ѧ��ÿ���Ķ�ʱ�������ƽ����![]() ����λ��
�����![]() ��
��![]() ��ֵ��ȷ��0.01����
��ֵ��ȷ��0.01����
��2��Ϊ����Ӱ��ѧ���Ķ�ʱ������أ�ѧУ��ί������ÿ���Ķ�ʱ��Ϊ![]() ��
��![]() ��ѧ���г�ȡ9���μ���̸�ᣮ����Ϊ9������Ӧ����ô���䣿��˵�����ɣ�
��ѧ���г�ȡ9���μ���̸�ᣮ����Ϊ9������Ӧ����ô���䣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ��
��![]()
![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ���е�.
���е�.
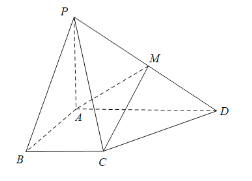
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����x��0��f��x���ļ�ֵ��.
����x��0��f��x���ļ�ֵ��.
��1����f��x������Сֵ��
��2���Ƿ����ʵ��b��ʹ�ù���x�IJ���ʽex��bx+f��x���ڣ�0��+�ޣ��Ϻ�����������ڣ����b��ȡֵ��Χ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ������ԭ��ΪԲ�ģ��Զ��᳤Ϊֱ����Բ
������ԭ��ΪԲ�ģ��Զ��᳤Ϊֱ����Բ![]() ����
����![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2��������![]()
![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ������Բ
������Բ![]() û�й����㣬��
û�й����㣬��![]() Ϊ��Բ
Ϊ��Բ![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() Ϊ����ԭ�㣩����ʵ��
Ϊ����ԭ�㣩����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ѽ۸�ָ�������CPI����һ����ӳ�����ͥһ�������������Ʒ�ͷ�����Ŀ�۸�ˮƽ�䶯����ĺ�۾���ָ��.һ����˵��CPI�ĸߵ�ֱ��Ӱ���Ź��ҵĺ�۾��õ��ش�ʩ�ij�̨�����ȣ���ͼ�ǹ���ͳ�ƾַ������ҹ�2009����2018����ʮ��������Ѽ۸�ָ��������ͼ.
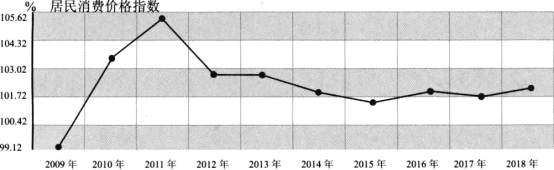
�����жԸ�����ͼ������ȷ���ǣ� ��
A.��ʮ��ľ������Ѽ۸�ָ������λ��Ϊ2013��ľ������Ѽ۸�ָ��
B.��ʮ��ľ������Ѽ۸�ָ��������Ϊ2015��ľ������Ѽ۸�ָ��
C.2009�ꡫ2012����4��������Ѽ۸�ָ���ķ���С��2015�ꡫ2018����4��������Ѽ۸�ָ���ķ���
D.2011�ꡫ2013����3��������Ѽ۸�ָ����ƽ��ֵ����2016�ꡫ2018����3��������Ѽ۸�ָ����ƽ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ŶӶ�![]() ���¹ڷ���ȷ�ﻼ�ߵ��ٴ����������˻ع��Է���.����
���¹ڷ���ȷ�ﻼ�ߵ��ٴ����������˻ع��Է���.����![]() �����̻����У���֢����Ϊ
�����̻����У���֢����Ϊ![]() �ˣ���֢����ԼΪ
�ˣ���֢����ԼΪ![]() ��
��![]() �������̻����У���֢����Ϊ
�������̻����У���֢����Ϊ![]() �ˣ���֢����Ϊ
�ˣ���֢����Ϊ![]() .�����������ݻ���
.�����������ݻ���![]() �����������£�
�����������£�
�������� | ���������� | �ܼ� | |
��֢���� | 30 | 120 | 150 |
��֢���� | 100 | 800 | 900 |
�ܼ� | 130 | 920 | 1050 |
(1)�������������ݣ��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ�¹ڷ�����֢�������йأ�
��ǰ������Ϊ�¹ڷ�����֢�������йأ�
(2)��֪ÿ����֢����ƽ�����Ʒ���ԼΪ![]() ��Ԫ��ÿ����֢����ƽ�����Ʒ���ԼΪ
��Ԫ��ÿ����֢����ƽ�����Ʒ���ԼΪ![]() ��Ԫ.��������ȷ�ﻼ��20�ˣ�����
��Ԫ.��������ȷ�ﻼ��20�ˣ�����![]() �����ߵ����Ʒ����ܺ�Ϊ
�����ߵ����Ʒ����ܺ�Ϊ![]() ����
����![]() .
.
����
|
|
|
|
|
|
|
|
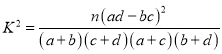
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com