
 ,随机猜对问题B的概率p2=
,随机猜对问题B的概率p2= ,
, ,P(ξ=m)=p1(1-p2)=
,P(ξ=m)=p1(1-p2)= ,
, .
. +m×
+m× +(m+n)×
+(m+n)× =
=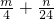 .
. ,P(η=n)=p2(1-p1)=
,P(η=n)=p2(1-p1)= ,
, .
. +n×
+n× +(m+n)×
+(m+n)× =
=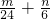 .
.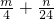 )-(
)-(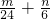 )=
)= ,
,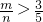 时,Eξ>Eη,先回答问题A,再回答问题B,获奖的期望值较大;
时,Eξ>Eη,先回答问题A,再回答问题B,获奖的期望值较大; =
= 时,Eξ=Eη,两种顺序获奖的期望值相等;
时,Eξ=Eη,两种顺序获奖的期望值相等; <
< 时,Eξ<Eη,先回答问题B,再回答问题A,获奖的期望值较大.
时,Eξ<Eη,先回答问题B,再回答问题A,获奖的期望值较大. ,随机猜对问题B的概率p2=
,随机猜对问题B的概率p2= ,回答问题的顺序有两种:(1)先回答问题A,再回答问题B.
,回答问题的顺序有两种:(1)先回答问题A,再回答问题B. ,P(ξ=m)=p1(1-p2)=
,P(ξ=m)=p1(1-p2)= ,P(ξ=m+n)=p1p2=
,P(ξ=m+n)=p1p2= .Eξ=0×
.Eξ=0× +m×
+m× +(m+n)×
+(m+n)× =
=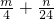 ;(2)先回答问题B,再回答问题A.参与者获奖金额η可取0,n,m+n.,则P(η=0)=1-p2=
;(2)先回答问题B,再回答问题A.参与者获奖金额η可取0,n,m+n.,则P(η=0)=1-p2= ,P(η=n)=p2(1-p1)=
,P(η=n)=p2(1-p1)= ,P(η=m+n)=p2p1=
,P(η=m+n)=p2p1= .Eη=0×
.Eη=0× +n×
+n× +(m+n)×
+(m+n)× =
=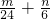 .由此能求出结果.
.由此能求出结果.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选项,但都只有一个选项是正确的。问题A回答正确可得奖金m元,问题B回答正确可得奖金n元。
活动规定:①参与者可任意选择答题顺序;②如果第一个问题回答错误则该参与者猜奖活动中止。
一个参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题,试确定回答问题的顺序,使获奖金额的期望值较大。
查看答案和解析>>
科目:高中数学 来源: 题型:
(必做题)(本小题满分10分)
电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选
项,但都只有一个选项是正确的。正确回答问题A可获奖金m元,正确回答问题B可获奖金n元。
活动规定:①参与者可任意选择回答问题的顺序;②如果第一个问题回答错误,则该参与者猜奖活动中止。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南通市海安高级中学高三(下)5月自检数学试卷(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com