
【题目】某化工厂一种溶液的成品,生产过程的最后工序是过滤溶液中的杂质,过滤初期溶液含杂质为2%,每经过一次过滤均可使溶液杂质含量减少![]() ,记过滤次数为x(
,记过滤次数为x(![]() )时溶液杂质含量为y.
)时溶液杂质含量为y.
(1)写出y与x的函数关系式;
(2)按市场要求,出厂成品杂质含量不能超过0.1%,问至少经过几次过滤才能使产品达到市场要求?(参考数据:![]() ,
,![]() )
)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b是异面直线,给出下列结论:
①一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
③一定存在无数个平面![]() ,使直线b与平面
,使直线b与平面![]() 交于一个定点,且直线
交于一个定点,且直线![]() 平面
平面![]() .
.
则所有正确结论的序号为( )
A.②③B.①③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
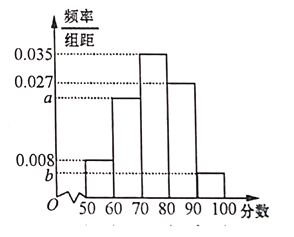
(1)求![]() 的值;
的值;
(2)若按照分层抽样从[50,60),[60,70)中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保险公司统计的资料表明:居民住宅区到最近消防站的距离x(单位:千米)和火灾所造成的损失数额y(单位:千元)有如下的统计资料:
距消防站距离x(千米) | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
火灾损失费用y(千元) | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明y与x有线性相关关系,试求:
(Ⅰ)求相关系数![]() (精确到0.01);
(精确到0.01);
(Ⅱ)求线性回归方程(精确到0.01);
(III)若发生火灾的某居民区与最近的消防站相距10.0千米,评估一下火灾的损失(精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
参考公式:相关系数  ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com