
分析 在数集的扩展过程中,有些性质是可以传递的,但有些性质不能传递,因此,要判断类比的结果是否正确,关键是要在新的数集里进行论证,当然要想证明一个结论是错误的,也可直接举一个反例,要想得到本题的正确答案,可对4个结论逐一进行分析,不难解答.
解答 解:①在复数集C中,z1,z2∈C,若z1-z2=0,则它们的实部和虚部均相等,则z1和z2相等.故①正确;
②若z1,z2∈C,当z1=1+i,z2=i时,z1-z2=1>0,但z1,z2 是两个虚数,不能比较大小.故②错误;
③由实数绝对值的性质|x|2=x2类比得到复数z的性质|z|2=z2,这两个长度的求法不是通过类比得到的,故③不正确,
故结论中,①是正确的.
故答案为:①.
点评 本题考查类比推理,是一个观察几个结论是不是通过类比得到,本题解题的关键在于对于所给的结论的理解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{12}$+kπ,$\frac{5π}{12}$+kπ](k∈Z) | B. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | ||
| C. | [-$\frac{2π}{3}$+4kπ,$\frac{4π}{3}$+4kπ](k∈Z) | D. | [-$\frac{5π}{6}$+4kπ,$\frac{7π}{6}$+4kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
已知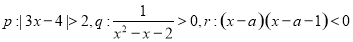 .
.
(1)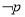 是
是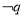 的什么条件?
的什么条件?
(2)若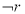 是
是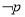 的必要非充分条件,求实数
的必要非充分条件,求实数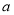 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com