
����Ŀ��ij��������ͬ����һ�ֲ�Ʒ�����ݼ�������ϸ��Ʒ������y��g����ߴ�x��mm��֮����������ϵʽy=axb��a��bΪ����0�ij��������������ȡ6���ϸ��Ʒ������������£�
�ߴ磨mm�� | 38 | 48 | 58 | 68 | 78 | 88 |
������g�� | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
���������˳������������ͳ������ֵ�����
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
�������������ݣ���y����x�Ļع鷽�̣�
������ij��ָ��ⶨ������Ʒ������ߴ�ı������䣨 ![]() ��
�� ![]() ����ʱΪ�ŵ�Ʒ���ִӳ�ȡ��6���ϸ��Ʒ������ѡ3�����Ǧ�Ϊȡ���ŵ�Ʒ�ļ�����������������εķֲ��к�������
����ʱΪ�ŵ�Ʒ���ִӳ�ȡ��6���ϸ��Ʒ������ѡ3�����Ǧ�Ϊȡ���ŵ�Ʒ�ļ�����������������εķֲ��к�������
��������һ�����ݣ�v1 �� u1������v2 �� u2����������vn �� un������ع�ֱ��u=��+��v��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ![]() =
= 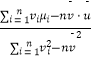 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺����y=axb��a��b��0������ȡ��ѧ������lny=blnx+lna��
��vi=lnxi��ui=lnyi��u=bv+lna��
�� 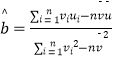 =
= ![]() ��
��
ln ![]() . =1��
. =1�� ![]() =e��
=e��
������ع鷽��Ϊ ![]() ��
��
������ 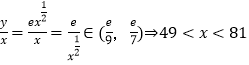 ��
��
58��68��78�����ŵ�Ʒ��3����
�εĿ���ȡֵ��0��1��2��3���� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��ֲ���Ϊ��
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
�� ![]() ��
��
����������1����y=axb��a��b��0������ȡ��ѧ������lny=blnx+lna������vi=lnxi��ui=lnyi��u=bv+lna������С���˷����ϵ�� ![]() ,��������ع鷽�̣���2��������ó��εĿ���ȡֵ��0��1��2��3���ֱ���ø��ʣ��г��ֲ��У������ѧ����.
,��������ع鷽�̣���2��������ó��εĿ���ȡֵ��0��1��2��3���ֱ���ø��ʣ��г��ֲ��У������ѧ����.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��= 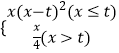 ����t��0��������g��x��=f[f��x����1]��6����ͬ����㣬��ʵ��t��ȡֵ��Χ�� ��
����t��0��������g��x��=f[f��x����1]��6����ͬ����㣬��ʵ��t��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������̨DEF��ABC�У�AB=2DE��G��H�ֱ�ΪAC��BC���е㣮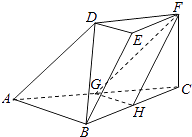
������֤��BD��ƽ��FGH��
������CF��ƽ��ABC��AB��BC��CF=DE����BAC=45�㣬��ƽ��FGH��ƽ��ACFD���ɵĽǣ���ǣ��Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����к졢�ơ���������ɫ��С���һ����ÿ�δ���ȡ��һ����������ɫ��Żأ���������ɫ����ȫ��ȡ��ʱֹͣȡ����ǡ��ȡ5����ʱֹͣȡ��ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y= ![]() ��y=ln��1��x���Ķ�����ֱ�ΪM��N����M��N=��������
��y=ln��1��x���Ķ�����ֱ�ΪM��N����M��N=��������
A.��1��2]
B.[1��2]
C.�����ޣ�1]�ȣ�2��+�ޣ�
D.�����ޣ�1����[2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��M����1��0����N��1��0������ijֱ���ϴ��ڵ�P��ʹ��|PM|+|PN|=4����Ƹ�ֱ��Ϊ������ֱ�ߡ�����������ֱ�ߣ���x��2y+6=0����x��y=0����2x��y+1=0����x+y��3=0�������ǡ�����ֱ�ߡ����ǣ�������
A.�٢�
B.�٢�
C.�ڢ�
D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��2��a����x��1����2lnx
��1����a=1ʱ����f��x���ĵ������䣻
��2��������f��x���ڣ�0�� ![]() ��������㣬��a��Сֵ��
��������㣬��a��Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A.��a��R���� ![]() ��1���ǡ�a��1���ı�Ҫ���������
��1���ǡ�a��1���ı�Ҫ���������
B.��p��qΪ�����⡱�ǡ�p��qΪ�����⡱�ı�Ҫ���������
C.������p����x��R��sinx+cosx�� ![]() ������Vp��������
������Vp��������
D.���⡰x0��R��ʹ��x02+2x0+3��0���ķ��ǡ�x��R��x2+2x+3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ��ԭ��OΪ���㣬x��������Ϊ���ᣬ������������ϵ��ȡ��ͬ�ij��ȵ�λ����ֱ֪��l�IJ�������Ϊ 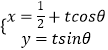 ����tΪ������0���ȣ��У�������C�ļ����귽��Ϊ��sin2����2cos��=0��
����tΪ������0���ȣ��У�������C�ļ����귽��Ϊ��sin2����2cos��=0��
��1��������C��ֱ�����귽�̣�
��2����ֱ��l������C�ཻ��A��B���㣬���ȱ仯ʱ����|AB|����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com