
����Ŀ��Ϊӭ��2022�걱���������˻ᣬ�ռ�����֪ʶ��ijУ��չ������ѩ������������֪ʶ��������ִӲμӶ���֪ʶ�������ѧ���������ȡ��100��ѧ���������ǵı����ɼ�������Ϊ100�֣���Ϊ6�飺![]() ��
��![]() �õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
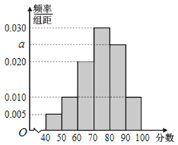
������![]() ��ֵ��
��ֵ��
����![]() ��ʾ�¼����ӲμӶ���֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80����������
��ʾ�¼����ӲμӶ���֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80����������![]() �ĸ��ʣ�
�ĸ��ʣ�
�����ڳ�ȡ��100��ѧ���У��涨�������ɼ�������80��Ϊ���������������ɼ�����80��Ϊ���������������ڴ���Ͻ�![]() �������������������ж��Ƿ���
�������������������ж��Ƿ���![]() �İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����
�İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����
�ο���ʽ�����ݣ�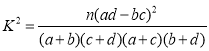 ��
��![]() ��
��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡�����![]() ����0.35����������û��
����0.35����������û��![]() �İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����
�İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����
��������
������Ƶ��ֱ��ͼ������С���ε����֮��Ϊ1��һ���ʽ�����⼴�ɣ�
����ϣ�1���Ľ��ۣ���������ɼ�������![]() �ֵ�Ƶ�ʼ��ɣ�
�ֵ�Ƶ�ʼ��ɣ�
����ϣ�2���Ľ��ۣ�����������ɼ�����������������������![]() ���������ٸ������������Ĺ�ʽ���
���������ٸ������������Ĺ�ʽ���![]() ��ֵ����ϲο����ݽ����жϼ���.
��ֵ����ϲο����ݽ����жϼ���.
�����������![]() �����
�����![]()
�����ɣ���֪![]() ��������ɼ�������80�ֵ�Ƶ��Ϊ
��������ɼ�������80�ֵ�Ƶ��Ϊ![]() ���ʴӲμӶ��»�֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80�ֵ�Ƶ��ԼΪ0.35
���ʴӲμӶ��»�֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80�ֵ�Ƶ��ԼΪ0.35
�����ɣ���֪���ڳ�ȡ��100��ѧ���У������ɼ�����![]() �ˣ�
�ˣ�
�ɴ˿ɵ�������![]() ��������
��������
���� | ������ | �ϼ� | |
���� | 10 | 40 | 50 |
�� | 25 | 25 | 50 |
�ϼ� | 35 | 65 | 100 |
����![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
����û��![]() �İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����
�İ�����Ϊ�������ɼ��Ƿ��������Ա��й�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B����Ʒ�Ƹ����ֳ���2017��7�µ���������(��2017��6�±Ƚ�)���������±���
AƷ�Ƴ��� | A1 | A2 | A3 | ||||
���������� | -7.29% | 10.47% | 14.70% | ||||
BƷ�Ƴ��� | B1 | B2 | B3 | ||||
���������� | -8.49% | -28.06% | 13.25% | ||||
���ݴ˱��е����ݣ������¹���7�·��������ĸ�����:��A1����������B1���������ࣻ
��AƷ�����ֳ������������������ʿ��ܴ���14.70%��
��BƷ����������������������ʿ���Ϊ����
��AƷ�����ֳ������������������ʿ���С��BƷ�����ֳ������������������ʣ�
������ȷ���۵ĸ�����( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A={x|x2��9}��B={x|��1��x��7}��C={x||x��2|��4}��
��1����A��B��A��C��
��2����U=R����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ֵ�����Ļ�������棬ֻ�з��š�![]() ���͡�
���͡�![]() ������ط������֣�ÿ���ӱ仯һ�Σ�ÿ�α仯ֻ���֡�
������ط������֣�ÿ���ӱ仯һ�Σ�ÿ�α仯ֻ���֡�![]() ���͡�
���͡�![]() ��֮һ�����г��֡�
��֮һ�����г��֡�![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() �����֡�
�����֡�![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() ������
������![]() �γ��֡�
�γ��֡�![]() �������
�������![]() ������
������![]() �γ��֡�
�γ��֡�![]() �������
�������![]() ����
����![]() .
.
��1����![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
��2����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() =1��2��3��4���ĸ���.
=1��2��3��4���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����
�������жϺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
����![]() ʱ������ʽ
ʱ������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ֱ��������������![]() ��
��![]() ��
��![]() .һֻ��Ȯ�ڵ�
.һֻ��Ȯ�ڵ�![]() ����һ����С��ֻ���Ӵӵ�
����һ����С��ֻ���Ӵӵ�![]() ����Ѩ����
����Ѩ����![]() ��ǰ�У�����������ȥ.�����ӷ�����Ȯ�Ϻ�æ����Ѩ���ܣ�����Ϊ������ٶȣ��ɵ���һֻС�ñ��ܣ��ٶȲ��䣬�ҵ��������С���������ʱ�䲻�ƣ�.��֪
��ǰ�У�����������ȥ.�����ӷ�����Ȯ�Ϻ�æ����Ѩ���ܣ�����Ϊ������ٶȣ��ɵ���һֻС�ñ��ܣ��ٶȲ��䣬�ҵ��������С���������ʱ�䲻�ƣ�.��֪![]() ��
��![]() ����Ȯ�����á�С�ñ��ܵ��ٶȷֱ�Ϊ
����Ȯ�����á�С�ñ��ܵ��ٶȷֱ�Ϊ![]() ��
��![]() ��
��![]() ������ǰ�е��ٶ�Ϊ
������ǰ�е��ٶ�Ϊ![]() .����ֻ�����������뿪��
.����ֻ�����������뿪��![]() ______
______![]() ʱ������Ȯ������ǡ����Ȯ���Լ�֮ǰȫ���ܽ���Ѩ.
ʱ������Ȯ������ǡ����Ȯ���Լ�֮ǰȫ���ܽ���Ѩ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() �Ǻ���
�Ǻ���![]() �ĵ�������
�ĵ�������
��1����![]() ����֤��������
����֤��������![]() ��
��![]() ��
��
��2��������![]() ��������ֵ�㣬��ʵ��
��������ֵ�㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������£�����Ʈ�㣬ij��Уӭ����һ���������ѧ���������Ӵ���ʵҲ�Ǻ���ṵͨ��һ��ƽ̨��У��ί��ѧ�������Уѧ���������ȡ��160��ѧ�������Ƿ�Ը��Ͷ�뵽�����Ӵ������������ʾ����飬ͳ���������£�
Ը�� | ��Ը�� | |
���� | 60 | 20 |
Ůʿ | 40 | 40 |
��1�������ϱ�˵�����ܷ���99%������ΪԸ��μ������Ӵ��������Ա��йأ�
��2���ִӲ����ʾ�������Ը��μ������Ӵ�������ѧ���У����ð��Ա�ֲ�����ķ�����ѡȡ5�ˣ�������5�������ѡȡ3�˵���վӭ����������ѡȡ��3����ǡ����1��Ů���ĸ���.
����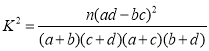 ������
������![]() ��
��
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ����
����![]() ����
����![]() ��Բ
��Բ![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]()
![]() �ֱ����߶�
�ֱ����߶�![]()
![]() �ϣ�������
�ϣ�������![]() ��
��![]() .
.
��1�����![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ���
���![]() �Ĺ켣�ཻ��
�Ĺ켣�ཻ��![]() ���㣬��
���㣬��![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ�ڱߵ�ƽ���ı��������Σ�������ڣ����
Ϊ�ڱߵ�ƽ���ı��������Σ�������ڣ����![]() ��ȡֵ��Χ����������ڣ�˵������.
��ȡֵ��Χ����������ڣ�˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com