【题目】某校在高二年级开设选修课，其中数学选修课开了三个班．选课结束后，有四名选修英语的同学要求改修数学，但数学选修每班至多可再接收两名同学，那么安排好这四名同学的方案有（ ）
A.72种
B.54种
C.36种
D.18种
科目：高中数学 来源： 题型：
【题目】某地西红柿从 
月 
日起开始上市．通过市场调查，得到西红柿种植成本 
(就是每 
公斤西红柿的种植成本，单位：元)与上市时间 
(单位：天)的数据如下表：
上市时间 | 50 | 110 | 250 |
种植成本 | 150 | 108 | 150 |
（1）根据上表数据，从下列函数中选取一个函数描述西红柿种植成本与上市时间 的变化关系： 
； 
； 
； 
，并求出函数解析式；
（2）利用你选取的函数，求西红柿种植成本最低时的上市天数及最低种植成本．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}的首项a1=1，前n项和为Sn ， 且S1 ， 
成等差数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}为递增的等比数列，且集合{b1 ， b2 ， b3}{a1 ， a2 ， a3 ， a4 ， a5}，设数列{anbn}的前n项和为Tn ， 求Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
+ 
=1（a＞b＞0）的左右焦点分别为F1 ， F2 ， 抛物线y2=4x与椭圆C有相同的焦点，且椭圆C过点 
． （I）求椭圆C的标准方程；
（Ⅱ）若椭圆C的右顶点为A，直线l交椭圆C于E、F两点（E、F与A点不重合），且满足AE⊥AF，若点P为EF中点，求直线AP斜率的最大值．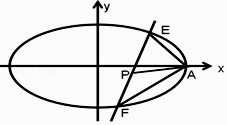
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直三棱柱ABC﹣A1B1C1 中，AA1=AB=AC=1，E，F分别是CC1、BC 的中点，AE⊥ A1B1 ， D为棱A1B1上的点．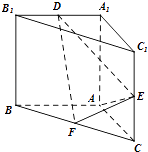
（1）证明：DF⊥AE；
（2）是否存在一点D，使得平面DEF与平面ABC所成锐二面角的余弦值为 
？若存在，说明点D的位置，若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设向量 
=（sinx，﹣1）， 
=（ 
cosx，﹣ 
），函数f（x）=（ + ） ．
（1）求函数f（x）的单调递增区间；
（2）当x∈（0， 
）时，求函数f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在锐角△ABC中，角A，B，C的对边分别为a，b，c，满足 
= 
．
（1）求角A的大小；
（2）若a= 
，△ABC的面积S△ABC=3 
，求b+c的值，；
（3）若函数f（x）=2sinxcos（x+ 
），求f（B）的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
