
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)去绝对值得分段函数: ,由单调性易求函数f(x)的最大值,即有M的值,再由柯西不等式,即可得到所求最小值;
,由单调性易求函数f(x)的最大值,即有M的值,再由柯西不等式,即可得到所求最小值;
(2)应用分析法证明,考虑两边取自然对数,结合因式分解和不等式的性质、对数的性质,即可得证.
解:(1)函数 ,
,
∴![]() 在(∞,1)上单调递增,在(1,+∞)上单调递减,
在(∞,1)上单调递增,在(1,+∞)上单调递减,
当x=1时,f(x)取得最大值![]() ,
,
即M=2,
正实数a,b满足a+b=2,
由柯西不等式可得(2a2+b2)(![]() 1)≥(
1)≥(![]() a
a![]() b)2,
b)2,
化为2a2+b2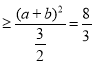 ,
,
所以当![]() ,即b
,即b![]() ,a
,a![]() 时,2a2+b2取得最小值
时,2a2+b2取得最小值![]() ;
;
(2)证明:因为a+b=2,a,b>0,要证aabb≥ab,即证alna+blnb≥lna+lnb,
即证(a﹣1)lna≥(1﹣b)lnb,
即证(a﹣1)lna≥(a﹣1)ln(2﹣a),
即证(1﹣a)ln(![]() 1)≥0,
1)≥0,
当0<a<1时,![]() 1>1,所以ln(
1>1,所以ln(![]() 1)>0,
1)>0,
由1﹣a>0,可得(1﹣a)ln(![]() 1)>0;
1)>0;
当a=1![]() 1)=0;
1)=0;
当1<a<2时,0![]() 1<1,所以ln(
1<1,所以ln(![]() 1)<0,
1)<0,
因为1﹣a<0,所以(1﹣a)ln(![]() 1)>0,
1)>0,
综上所述,(1﹣a)ln(![]() 1)≥0成立,即aabb≥ab.
1)≥0成立,即aabb≥ab.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情造成医用防护服紧缺,当地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到![]() (万件),其中k为工厂工人的复工率
(万件),其中k为工厂工人的复工率![]() ,A公司生产t万件防护服还需投入成本
,A公司生产t万件防护服还需投入成本![]() (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的![]() (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() (
(![]() 为正常数),
为正常数),![]() 为
为![]() 轴负半轴上的一个动点,动点
轴负半轴上的一个动点,动点![]() 满足
满足![]() ,且线段
,且线段![]() 的中点在
的中点在![]() 轴上.
轴上.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 的一条动弦(
的一条动弦(![]() 不垂直于
不垂直于![]() 轴).其垂直平分线与
轴).其垂直平分线与![]() 轴交于点
轴交于点![]() .当
.当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,![]() .
.
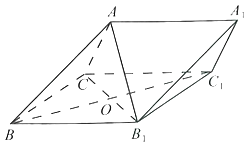
(1)求证:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且点A在侧面BB1C1C上的投影为点O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线
,过右焦点F的直线l与椭圆E交于A,B两点(A,B两点不在x轴上),椭圆E在A,B两点处的切线交于P,点P在定直线![]() 上.
上.
(1)记点![]() ,求过点
,求过点![]() 与椭圆E相切的直线方程;
与椭圆E相切的直线方程;
(2)以![]() 为直径的圆过点F,求
为直径的圆过点F,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,P,Q,M,N,H,R是各条棱的中点.
中,P,Q,M,N,H,R是各条棱的中点.
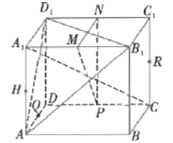
①直线![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四点共面;④
;③P,Q,H,R四点共面;④![]() 平面
平面![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com