
����Ŀ�����Ӵ�ý��˾Ϊ�˽�ij�������ӹ��ڶ�ij��������Ŀ����������������ȡ��100�����ڽ��е���.�����Ǹ��ݵ��������ƵĹ����վ��տ���������Ŀʱ���Ƶ�ʷֲ�ֱ��ͼ��


���վ��տ���������Ŀʱ�䲻����40���ӵĹ��ڳ�Ϊ�������ԡ�.
��1��������֪������������![]() ������������
������������![]() �Ŀɿ���Ҫ���ݴ����ϣ����Ƿ���Ϊ�������ԡ����Ա��йأ�
�Ŀɿ���Ҫ���ݴ����ϣ����Ƿ���Ϊ�������ԡ����Ա��йأ�
��2���������������õ���Ƶ����Ϊ����.���ڴӸõ����������ӹ����У����������������ÿ�γ�ȡ1�����ڣ���ȡ3�Σ��DZ���ȡ��3�������еġ������ԡ�����Ϊ![]() .��ÿ�γ�ȡ�Ľ����������ģ���
.��ÿ�γ�ȡ�Ľ����������ģ���![]() �ֲ��У�����
�ֲ��У�����![]() �ͷ���
�ͷ���![]() .
.
���� 

���𰸡���1��û�����ɣ�2��������
�������������������1������Ƶ�ʷֲ�ֱ��ͼ���ɵø�����ʣ���һ������������������ù�ʽ���![]() ��ֵ������������ݣ��ö����Լ���ɵý������2�����÷ֲ��������ȷ��
��ֵ������������ݣ��ö����Լ���ɵý������2�����÷ֲ��������ȷ��![]() ������
������![]() ��
��![]() Ů�����ùŵ���ͣ��ɵý����
Ů�����ùŵ���ͣ��ɵý����
���������(1)��Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У��������ԡ���25�ˣ��Ӷ�![]() ���������£�
���������£�
�������� | ������ | �ϼ� | |
�� | 30 | 15 | 45 |
Ů | 45 | 10 | 55 |
�ϼ� | 75 | 25 | 100 |
��![]() �������е����ݴ��빫ʽ���㣬��
�������е����ݴ��빫ʽ���㣬��

![]() .
.
��Ϊ![]() ������û��������Ϊ�������ԡ����Ա��йأ�
������û��������Ϊ�������ԡ����Ա��йأ�
(2)�ɷֲ������֪![]() ��������ռ
��������ռ![]() ��Ů��ռ
��Ů��ռ![]() ��ѡ
��ѡ![]() ��û��һ��Ů���ĸ���Ϊ
��û��һ��Ů���ĸ���Ϊ![]() ��������ȡ��2��������������һ��Ů���ĸ���Ϊ
��������ȡ��2��������������һ��Ů���ĸ���Ϊ![]() ��
��


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��x��A����A={x|a��1��x��a+1}������q��x��B����B={x|x2��4x+3��0}
������A��B=��A��B=R����ʵ��a��ֵ��
������p��q�ij����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij�洬�����O����ƫ��60�����������Լ160�����B���������飬��ʱ����۵����Ϸ�ǡ����һ�ܺ���Ѳ�߷ɻ�A�ӵ��洬������źţ�����Ѳ�߷ɻ�Ѹ�ٽ����֪ͨ����C������������Ҫ����Ѹ�ٸ������µص�ʩ�ȣ�������Ѳ�߷ɻ�����洬B�ĸ���Ϊ68.20�������������C�ĸ���Ϊ63.43������������λ���洬�ı�ƫ��60�������ϣ�
����������������C�����O�ľ��룻
����������������ÿСʱ25������ٶ�ֱ����ʻ���ܷ���3Сʱ�ڸϵ����µص㣿
���ο����ݣ�sin68.20���0.93��tan68.20���2.50��shin63.43���0.90��tan63.43���2.00�� ![]() ��3.62��
��3.62�� ![]() ��3.61��
��3.61��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
����![]() ʱ��������
ʱ��������![]() ��
��![]() �������߷��̣�
�������߷��̣�
����![]() ʱ�����ۺ���
ʱ�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
������б��Ϊ![]() ��ֱ���뺯��
��ֱ���뺯��![]() ��ͼ����
��ͼ����![]() ��
�� ![]() ���㣬����
���㣬����![]() ����֤��
����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͳ�ƾ־�ij�ؾ���������������10 000�ˣ��������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��(ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ[1 000��1 500)��

��1�������������[2000,3 000)��Ƶ�ʣ�
��2������Ƶ�ʷֲ�ֱ��ͼ����������ݵ���λ����
��3��Ϊ�˷�����������������䡢ְҵ�ȷ���Ĺ�ϵ�����밴�������ٴ���10 000���а��ֲ�����������100������һ������������������[2 000,3 000)�����Ӧ��ȡ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ������������ԭ��Ϊ���㣬
Ϊ������������ԭ��Ϊ���㣬 ![]() ��������Ϊ����ļ�����ϵ�У�ֱ��
��������Ϊ����ļ�����ϵ�У�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
��1��������![]() ����ͨ���̺�ֱ��
����ͨ���̺�ֱ��![]() ����б�ǣ�
����б�ǣ�
��2�����![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ���е㣮
���е㣮
������֤��![]() ƽ��
ƽ��![]() ��
��
������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
�������������ⳤΪ![]() ��������
��������![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
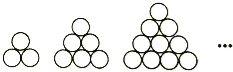
����Ŀ����Ԫʱ�ڽܳ�����ѧ��������������ѧ��������Ԫ����������������ζ�����һ�������������������ٰ�ʮ������������һ�����ʣ�ͬ�⣩֮���ʵ��ӣ�ÿ�������α������������ȼ��ڲ��������Σ�����̽���������������е���һ�ζ⣨����һ��������ָ����1������һ��3��������һ��6���������������ĶѶ⣬��Ҳ�����Ƕ⣬��ͼ����ʾ�ڶ��㿪ʼ��ÿ�������������������������Ƕ�ײ�����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C����Ӧ�ı�Ϊa��b��c
��1���� ![]() ����A��ֵ��
����A��ֵ��
��2���� ![]() ���ҡ�ABC�����
���ҡ�ABC����� ![]() ����sinC��ֵ��
����sinC��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com