
分析 (1)先求导,函数为单调函数,则f′(x)>0或f′(x)<0在x∈R恒成立,设g(x)=-x2+(2-a)x+a,通过二次函数的性质得到g(x)>0或g(x)<0,问题得以判断;
(2)f(x)=2在(0,1)内有解,转化为a=$\frac{2{e}^{x}}{x}$-x在(0,1)内有解,构造函数h(x)=$\frac{2{e}^{x}}{x}$-x,利用导数求出函数h(x)的值域即可.
解答 解:(1)f′(x)=(2x+a)e-x-(x2+ax)e-x=e-x[-x2+(2-a)x+a],
∵e-x>0恒成立,
设g(x)=-x2+(2-a)x+a,则g(x)开口向下,且△=(2-a)2+4a=(a+2)2≥0,
∴g(x)>0或g(x)<0,
∴f′(x)>0或f′(x)<0,
∴f(x)在x∈R上有增有减,
故判断f(x)在x∈R上不为单调函数.
(2)f(x)=(x2+ax)e-x=2在(0,1)内有解,
∴a=$\frac{2{e}^{x}}{x}$-x在(0,1)内有解,
令h(x)=$\frac{2{e}^{x}}{x}$-x,
∴h′(x)=$\frac{2{e}^{x}(x-1)}{{x}^{2}}$-1<0在(0,1)恒成立,
∴h(x)在(0,1)上单调递减,
∴h(1)<h(x)<h(0),
即2e-1<h(x)<+∞,
∴a>2e-1,
∴a的取值范围为(2e-1,+∞)
点评 本题主要考查通过求函数的导数来确定函数增减区间的问题,培养了学生的化归能力,运算能力,属于中档题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
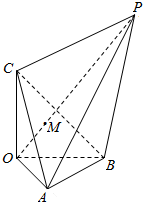 如图所示,已知三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.
如图所示,已知三棱锥O-ABC的三条侧棱OA、OB、OC两两垂直,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
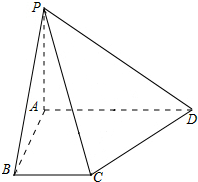 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
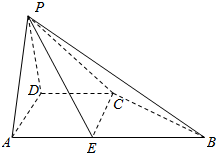 在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=$\frac{1}{2}$AB,∠ADC=120°
在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=$\frac{1}{2}$AB,∠ADC=120°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
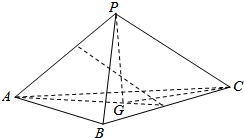 三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).
三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
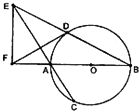 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com