
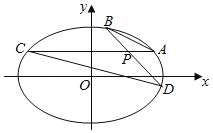
【题目】已知椭圆![]() ,倾斜角为
,倾斜角为![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .过椭圆
.过椭圆![]() 内一点
内一点![]() 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点![]() ,且满足
,且满足![]() ,其中
,其中![]() 为实数.当直线
为实数.当直线![]() 平行于
平行于![]() 轴时,对应的
轴时,对应的![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,
变化时,![]() 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)将M和N点坐标代入椭圆方程,根据斜率公式求得kMN=1,求得a和b的关系,当直线AP平行于x轴时,设|AC|=2d,求得A点坐标,代入椭圆方程,即可求得a和b,求得椭圆方程;
(Ⅱ)设出A、B、C和D点坐标,由向量共线,![]() =λ
=λ![]() ,
,![]() =λ
=λ![]() ,及A和B在椭圆上,利用斜率公式,kAB=kCD,求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB为定值.
,及A和B在椭圆上,利用斜率公式,kAB=kCD,求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB为定值.
(Ⅰ)设M(m1,n1)、N(m2,n2),则 ,
,
两式相减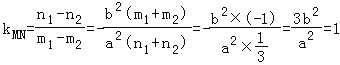 ,
,
故a2=3b2
当直线AP平行于x轴时,设|AC|=2d,
∵![]() ,
,![]() ,则
,则![]() ,解得
,解得![]() ,
,
故点A(或C)的坐标为![]() .
.
代入椭圆方程![]() ,得
,得![]()
a2=3,b2=1,
所以方程为![]() .
.
(Ⅱ)设A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)
由于![]() ,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
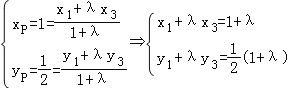 …①
…①
同理![]() 可得
可得 …②
…②
由①②得: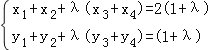 …③
…③
将点A、B的坐标代入椭圆方程得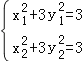 ,
,
两式相减得(x1+x2)(x1﹣x2)+3(y1+y2)(y1﹣y2)=0,
于是3(y1+y2)kAB=﹣(x1+x2)…④
同理可得:3(y3+y4)kCD=﹣(x3+x4),
于是3(y3+y4)kAB=﹣(x3+x4)(∵AB∥CD,∴kAB=kCD)
所以3λ(y3+y4)kAB=﹣λ(x3+x4)…⑤
由④⑤两式相加得到:3[y1+y2+λ(y3+y4)]kAB=﹣[(x1+x2)+λ(x3+x4)]
把③代入上式得3(1+λ)kAB=﹣2(1+λ),
解得:![]() ,
,
当λ变化时,kAB为定值,![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,椭圆的右顶点为
,椭圆的右顶点为![]() .
.
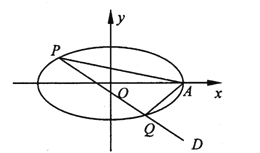
(1)求该椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于两个不同点
交椭圆于两个不同点![]() ,求证:直线
,求证:直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数,![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代一部重要的数学著作,书中有如下问题:“今有良马与驽马发长安,至齐.齐去长安三千里,良马初日行一百九十三里,日增一十三里,驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马,问几何日相逢.”其大意为:“现在有良马和驽马同时从长安出发到齐去,已知长安和齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里,驽马第一天行97里,之后每天比前一天少行0.5里.良马到齐后,立刻返回去迎驽马,多少天后两马相遇.”试确定离开长安后的第天,两马相逢.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的方程x2﹣ax﹣1=0和x2﹣x﹣2a=0的实根分别为x1、x2和x3、x4 , 若x1<x3<x2<x4 , 则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为 ![]() ,且∠AA1C1为锐角.
,且∠AA1C1为锐角.
(I) 求证:AA1⊥BC1;
(Ⅱ)求锐二面角B﹣AC﹣C1的余弦值.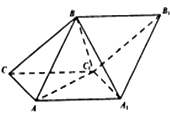
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点Q为对角面A1BCD1内一动点,点M、N分别在直线AD和AC上自由滑动,直线DQ与MN所成角的最小值为θ,则下列结论中正确的是( )
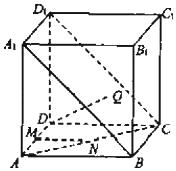
A. 若θ=15°,则点Q的轨迹为椭圆的一部分
B. 若θ=30°,则点Q的轨迹为椭圆的一部分
C. 若θ=45°,则点Q的轨迹为椭圆的一部分
D. 若θ=60°,则点Q的轨迹为椭圆的一部分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com